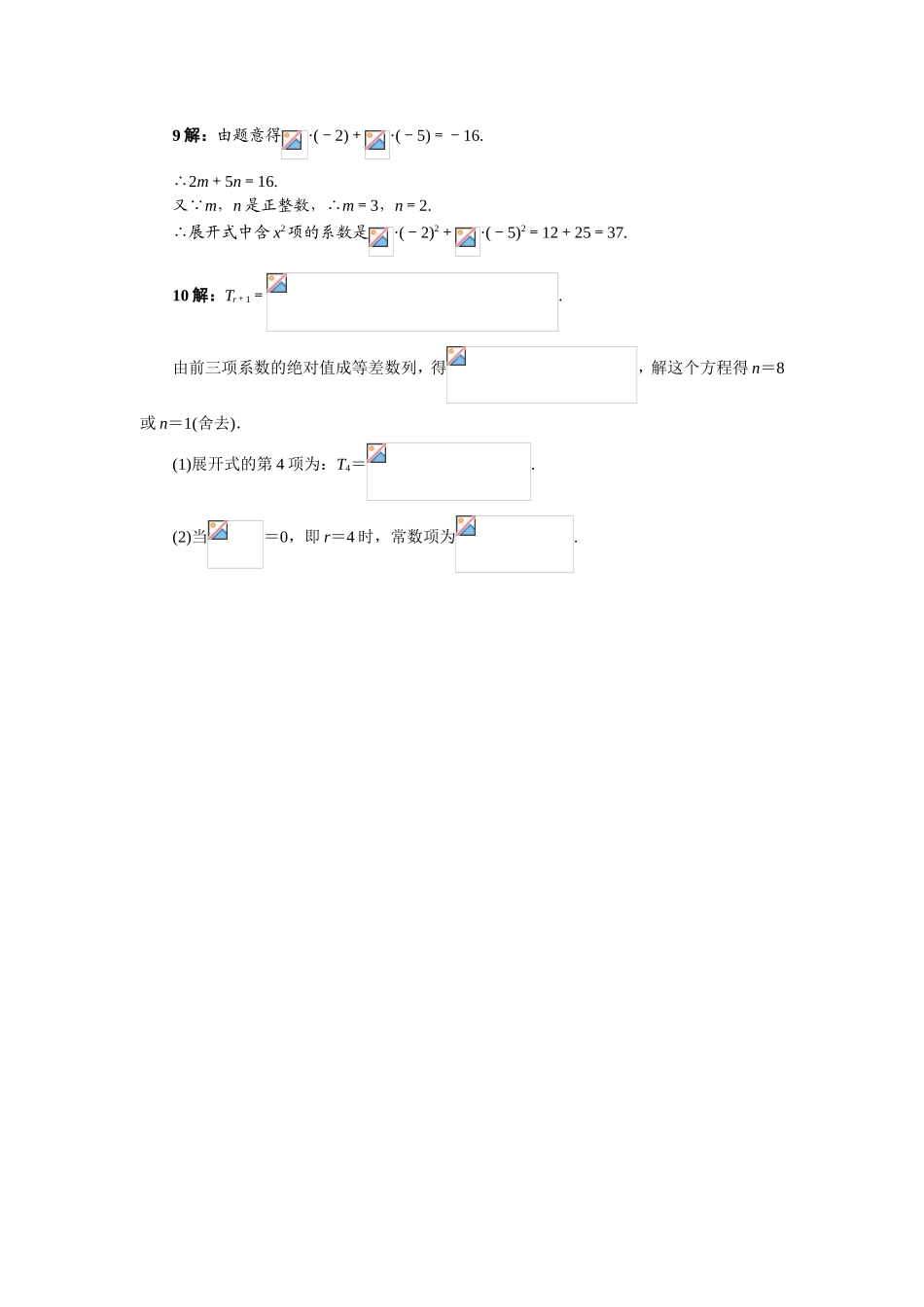
1.3.1二项式定理练习一、选择题1.·2n+·2n-1+…+·2n-k+…+等于().A.2nB.2n-1C.3nD.12.(2012山东济南一中期末,理2)(1-i)10(i为虚数单位)的二项展开式中第七项为().A.-210B.210C.-120iD.-210i3.展开式中x3的系数为10,则a的值等于().A.-1B.C.1D.24.(2012安徽高考,理7)(x2+2)的展开式的常数项是().A.-3B.-2C.2D.35.若x+x2+…+xn能被7整除,则x,n的值可能为().A.x=5,n=5B.x=5,n=4C.x=4,n=4D.x=4,n=3二、填空题6.(x3+2x)7的展开式中第4项的二项式系数是__________,第4项的系数是__________.7.(2012浙江高考,理14)若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a3=__________.8.设二项式(a>0)的展开式中x3的系数为A,常数项为B.若B=4A,则a的值是________.三、解答题9.设m,n是正整数,整式f(x)=(1-2x)m+(1-5x)n中含x的一次项的系数为-16,求含x2项的系数.10.在二项式的展开式中,前三项系数的绝对值成等差数列.(1)求展开式的第四项;(2)求展开式的常数项.参考答案1答案:C解析:原式=(2+1)n=3n.2答案:A解析:由通项公式得T7=·(-i)6==-210.3答案:D解析:展开式的通项公式Tr+1=·x5-r·=ar·x5-2r,令5-2r=3,∴r=1.∵x3的系数为10,∴a=10.∴a=2.4答案:D解析:的通项为Tr+1=(-1)r=(-1)r.要使(x2+2)的展开式为常数,须令10-2r=2或0,此时r=4或5.故(x2+2)的展开式的常数项是(-1)4×+2×(-1)5×=3.5答案:B解析:+…+=(1+x)n-1,检验得B正确.6答案:35280解析:因为(x3+2x)7的展开式的第4项是T4=(x3)4(2x)3,故该项的二项式系数是=35,该项的系数是23=280.7答案:10解析:由x5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5可得,可解得8答案:2解析:Tr+1==(-a)r,所以6-r=3时,r=2,所以A=15a2,6-r=0时,r=4,所以B=15a4,所以15a4=4×15a2,所以a2=4,又a>0,得a=2.9解:由题意得·(-2)+·(-5)=-16.∴2m+5n=16.又∵m,n是正整数,∴m=3,n=2.∴展开式中含x2项的系数是·(-2)2+·(-5)2=12+25=37.10解:Tr+1=.由前三项系数的绝对值成等差数列,得,解这个方程得n=8或n=1(舍去).(1)展开式的第4项为:T4=.(2)当=0,即r=4时,常数项为.