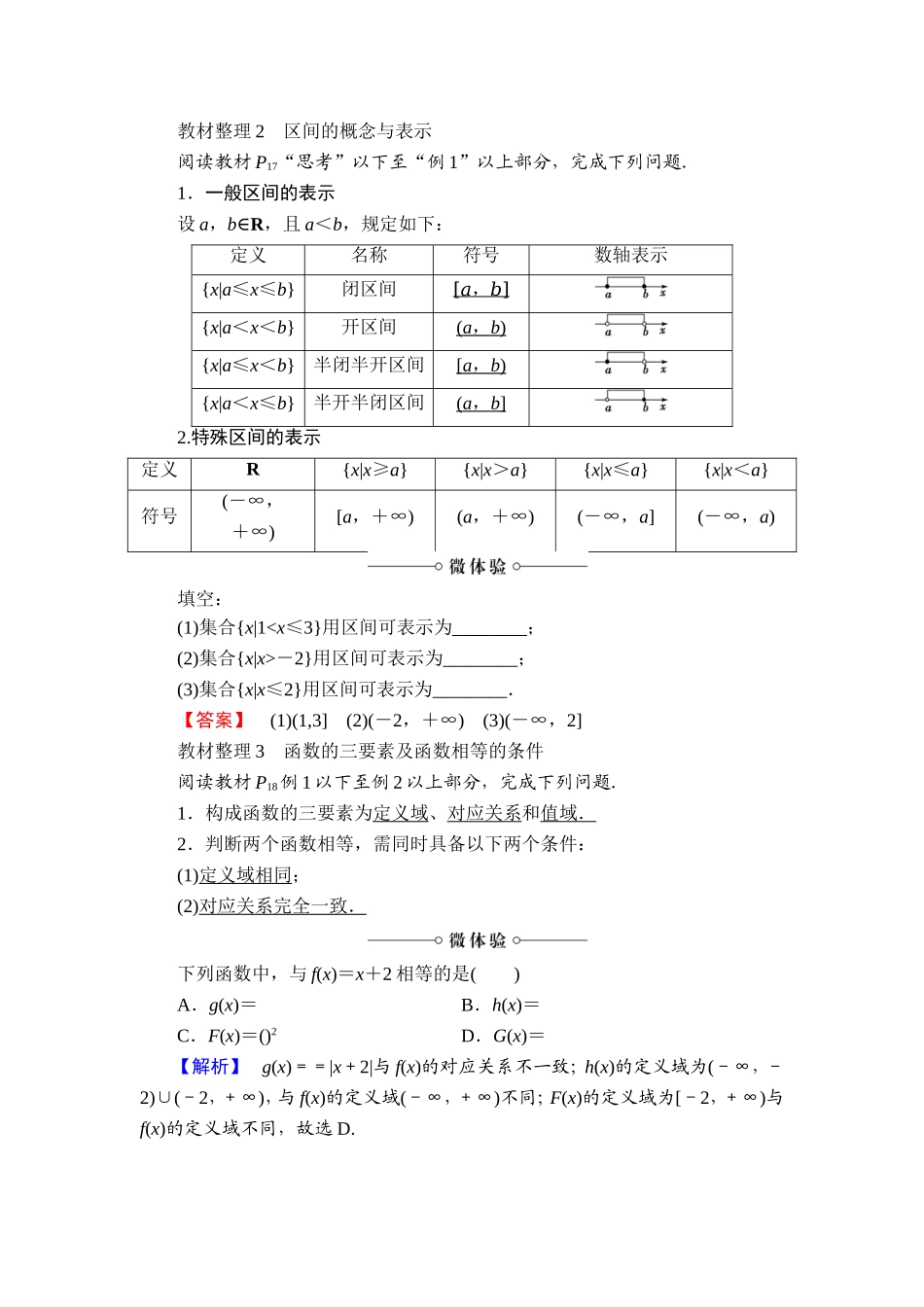
1.2.1函数的概念1.进一步体会函数是描述变量之间的依赖关系的重要数学模型.能用集合与对应的语言刻画出函数,体会对应关系在刻画数学概念中的作用.(重点、难点)2.了解构成函数的要素,会求一些简单函数的定义域和值域.(重点)3.能够正确使用区间表示数集.(易混点)[基础·初探]教材整理1函数的相关概念阅读教材P15~P17“思考”,完成下列问题.函数的有关概念函数值的集合判断(正确的打“√”,错误的打“×”)(1)任何两个集合之间都可以建立函数关系.()(2)根据函数的定义,定义域中的任何一个x可以对应着值域中不同的y.()(3)在函数的定义中,集合B是函数的值域.()【解析】(1)×.任何两个非空数集之间都可以建立函数关系.(2)×.根据函数的定义,对于定义域中的任何一个x,在值域中都有唯一确定的y与之对应.(3)×.在函数的定义中,函数的值域是集合B的子集.【答案】(1)×(2)×(3)×教材整理2区间的概念与表示阅读教材P17“思考”以下至“例1”以上部分,完成下列问题.1.一般区间的表示设a,b∈R,且a<b,规定如下:定义名称符号数轴表示{x|a≤x≤b}闭区间[a,b]{x|a<x<b}开区间(a,b){x|a≤x<b}半闭半开区间[a,b){x|a<x≤b}半开半闭区间(a,b]2.特殊区间的表示定义R{x|x≥a}{x|x>a}{x|x≤a}{x|x<a}符号(-∞,+∞)[a,+∞)(a,+∞)(-∞,a](-∞,a)填空:(1)集合{x|1-2}用区间可表示为________;(3)集合{x|x≤2}用区间可表示为________.【答案】(1)(1,3](2)(-2,+∞)(3)(-∞,2]教材整理3函数的三要素及函数相等的条件阅读教材P18例1以下至例2以上部分,完成下列问题.1.构成函数的三要素为定义域、对应关系和值域.2.判断两个函数相等,需同时具备以下两个条件:(1)定义域相同;(2)对应关系完全一致.下列函数中,与f(x)=x+2相等的是()A.g(x)=B.h(x)=C.F(x)=()2D.G(x)=【解析】g(x)==|x+2|与f(x)的对应关系不一致;h(x)的定义域为(-∞,-2)∪(-2,+∞),与f(x)的定义域(-∞,+∞)不同;F(x)的定义域为[-2,+∞)与f(x)的定义域不同,故选D.【答案】D[小组合作型]函数的概念(1)下列四个图象中,不是函数图象的是()(2)下列各组函数是同一函数的是()【导学号:97030025】①f(x)=与g(x)=x;②f(x)=x与g(x)=;③f(x)=x0与g(x)=;④f(x)=x2-2x-1与g(t)=t2-2t-1.A.①②B.①③C.③④D.①④(3)判断下列对应是否为函数:①x→y,y=,x≠0...