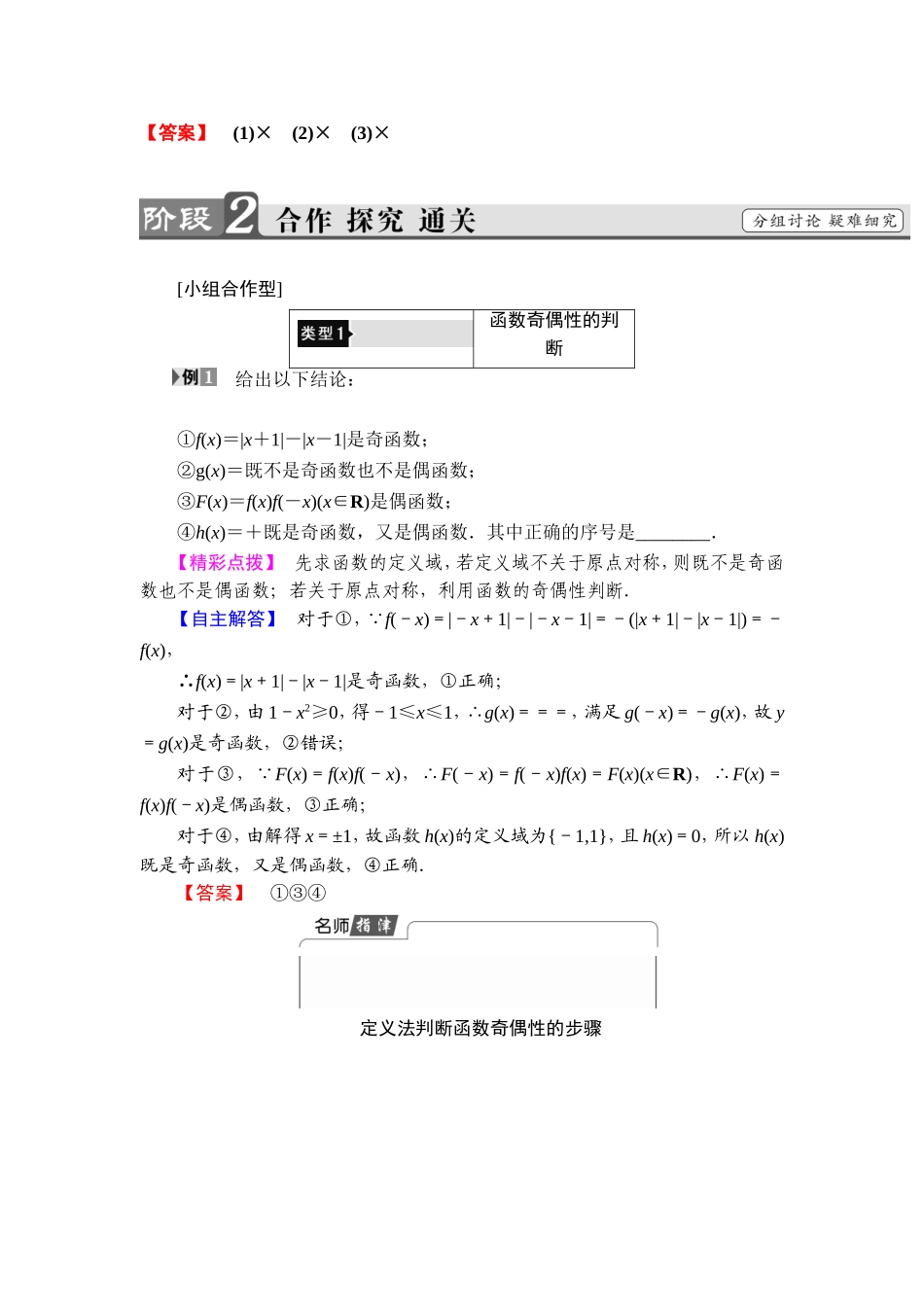
1.3.2奇偶性1.结合具体函数了解函数奇偶性的含义.(难点)2.会判断函数奇偶性的方法.(重点、难点)3.能运用函数图象理解和研究函数的奇偶性,了解函数奇偶性与图象的对称性之间的关系.(易混点)[基础·初探]教材整理1偶函数阅读教材P33~P34“观察”以上部分,完成下列问题.偶函数条件对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x)结论函数f(x)叫做偶函数图象特征偶函数的图象关于y轴对称,图象关于y轴对称的函数一定是偶函数.已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图134所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间.图134【解】由题意做出函数图象如下:据图可知,单调增区间为(-1,0),(1,+∞).教材整理2奇函数阅读教材P34“观察”至P35“例5”以上部分,完成下列问题.奇函数条件对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x)结论函数f(x)叫做奇函数图象特征奇函数的图象关于原点对称,图象关于原点对称的函数一定是奇函数.判断(正确的打“√”,错误的打“×”)(1)对于函数y=f(x),若存在x,使f(-x)=-f(x),则函数y=f(x)一定是奇函数.()(2)不存在既是奇函数,又是偶函数的函数.()(3)若函数的定义域关于原点对称,则这个函数不是奇函数就是偶函数.()【解析】(1)×.如f(x)=x2,满足f(-0)=-f(0)=0,但函数f(x)=x2不是奇函数.(2)×.存在f(x)=0,x∈R既是奇函数,又是偶函数.(3)×.函数f(x)=x2-2x,x∈R的定义域关于原点对称,但它既不是奇函数,也不是偶函数.【答案】(1)×(2)×(3)×[小组合作型]函数奇偶性的判断给出以下结论:①f(x)=|x+1|-|x-1|是奇函数;②g(x)=既不是奇函数也不是偶函数;③F(x)=f(x)f(-x)(x∈R)是偶函数;④h(x)=+既是奇函数,又是偶函数.其中正确的序号是________.【精彩点拨】先求函数的定义域,若定义域不关于原点对称,则既不是奇函数也不是偶函数;若关于原点对称,利用函数的奇偶性判断.【自主解答】对于①, f(-x)=|-x+1|-|-x-1|=-(|x+1|-|x-1|)=-f(x),∴f(x)=|x+1|-|x-1|是奇函数,①正确;对于②,由1-x2≥0,得-1≤x≤1,∴g(x)===,满足g(-x)=-g(x),故y=g(x)是奇函数,②错误;对于③, F(x)=f(x)f(-x),∴F(-x)=f(-x)f(x)=F(x)(x∈R),∴F(x)=f(x)f(-x)是偶函数,③正确;对于④,由解得x=±1,故函数h(x)的定义域为{-1,1},且h...