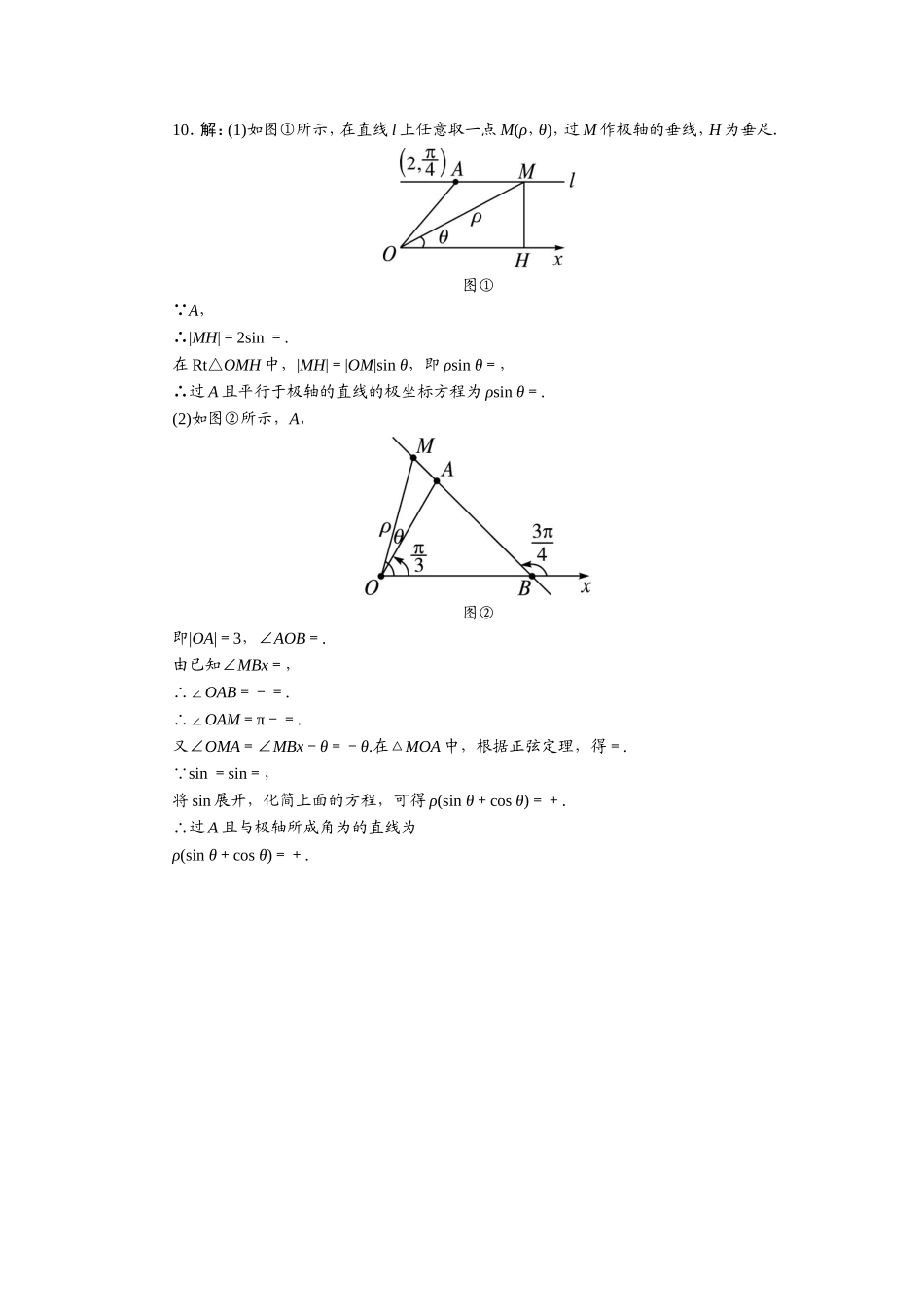
自我小测1.在极坐标系中,圆ρ=2sinθ的圆心到极轴的距离为()A.1B.C.D.22.在极坐标系中,过点P且垂直于极轴的直线方程为()A.ρcosθ=B.ρsinθ=C.ρ=cosθD.ρ=sinθ3.在极坐标系中,点F(1,0)到直线θ=(ρ∈R)的距离是()A.B.C.1D.4.极坐标方程分别是ρ=cosθ和ρ=sinθ的两个圆的圆心距是()A.2B.C.1D.5.在极坐标系中,过点A(6,π)作圆ρ=-4cosθ的切线,则切线长为()A.2B.6C.2D.26.已知圆的极坐标方程为ρ=4cosθ,圆心为C,点P的极坐标为,则|CP|=__________.7.在极坐标系中,曲线C1与C2的方程分别为2ρcos2θ=sinθ与ρcosθ=1.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1与C2交点的直角坐标为________.8.已知曲线C1:ρ=2和曲线C2:ρcos=,则C1上到C2的距离等于的点的个数为__________.9.求极坐标方程ρ=所对应的直角坐标方程.10.求:(1)过A且平行于极轴的直线的极坐标方程;(2)过A且与极轴所成的角为的直线的极坐标方程.参考答案1.解析:圆ρ=2sinθ的直角坐标方程为x2+y2=2y,即x2+(y-1)2=1.所以圆心坐标为(0,1).故圆心到极轴的距离为1.答案:A2.解析:设直线与极轴的交点为A,则|OA|=|OP|·cos=.又设直线上任意一点M(ρ,θ),则|OM|·cosθ=|OA|,即ρcosθ=.答案:A3.解析:因为直线θ=(ρ∈R)的直角坐标方程为y=x,即x-y=0,所以点F(1,0)到直线x-y=0的距离为.答案:A4.解析:如图所示,两圆的圆心的极坐标分别是和,这两点间的距离是.答案:D5.解析:如图,切线长为=2.答案:C6.解析:由圆的极坐标方程为ρ=4cosθ,得圆心C的直角坐标为(2,0),点P的直角坐标为(2,2),所以|CP|=2.答案:27.解析:曲线C1的直角坐标方程为y=2x2,曲线C2的直角坐标方程为x=1,联立解得因此交点的直角坐标为(1,2).答案:(1,2)8.解析:将方程ρ=2与ρcos=化为直角坐标方程得x2+y2=(2)2与x-y-2=0,知C1为圆心在坐标原点,半径为2的圆,C2为直线,因圆心到直线x-y-2=0的距离为,故满足条件的点的个数为3.答案:39.解:因为ρ=可化为ρ=,即ρ=.去分母,得ρ=2+ρcosθ.两边平方并将互化公式代入,得x2+y2=(2+x)2.整理可得y2=4(x+1).10.解:(1)如图①所示,在直线l上任意取一点M(ρ,θ),过M作极轴的垂线,H为垂足.图① A,∴|MH|=2sin=.在Rt△OMH中,|MH|=|OM|sinθ,即ρsinθ=,∴过A且平行于极轴的...