2016-2017学年人教A版选修2-1 3.2立体几何中的向量法 学案.doc

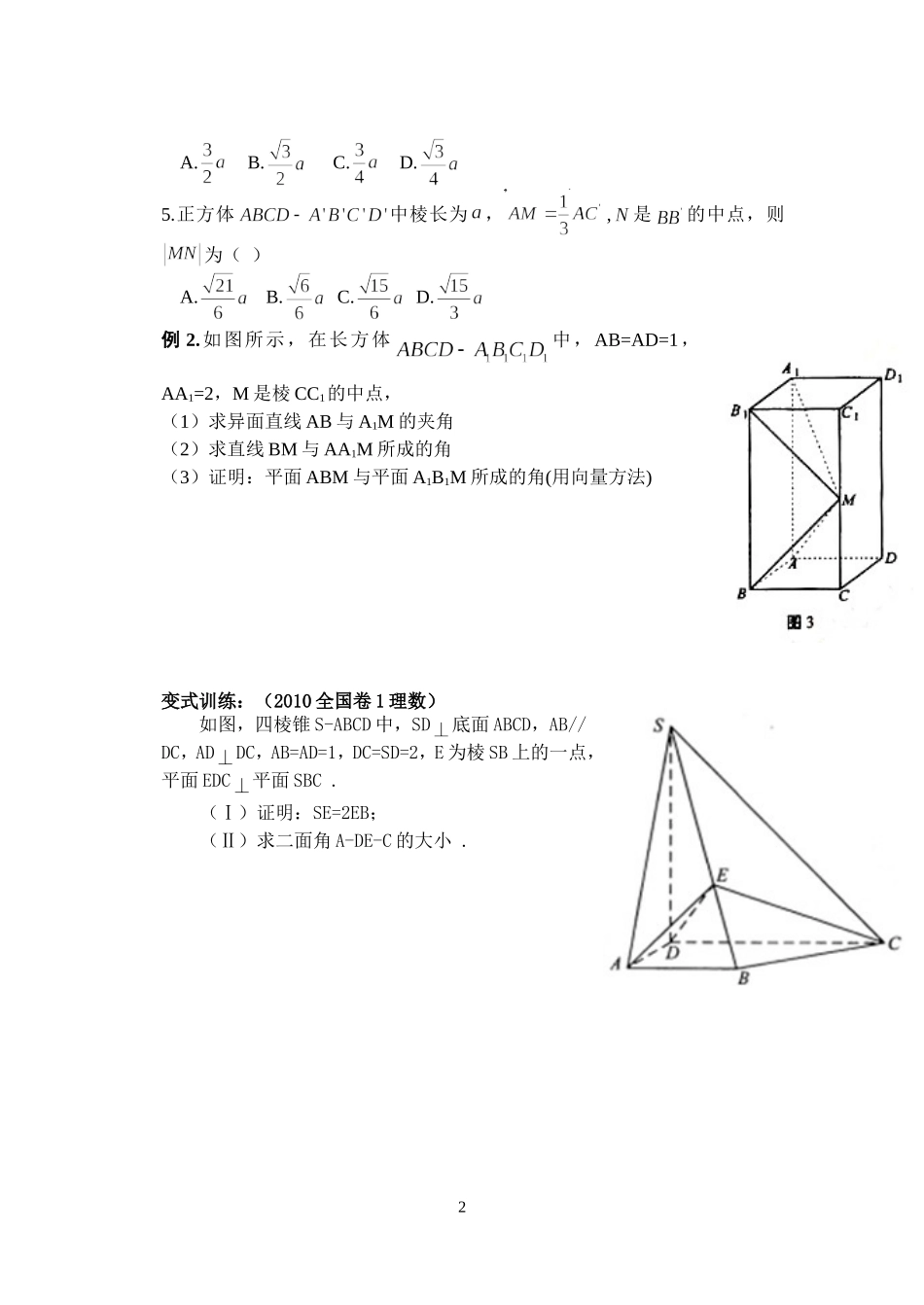
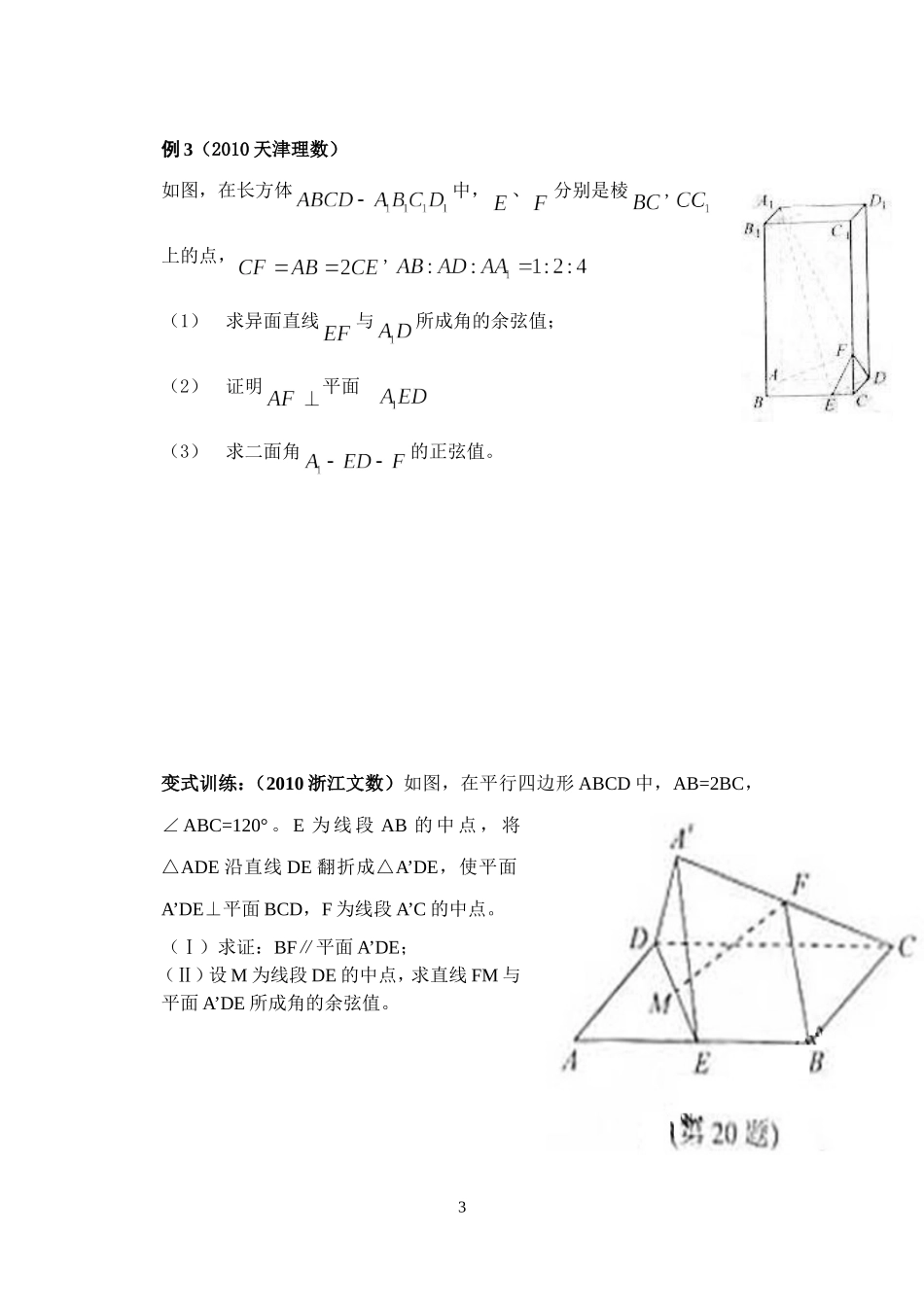
3.2.1 立体几何中的向量方法（1） ____之求角 【使用说明及学法指导】 1．先自学课本，理解概念，完成导学提纲； 2．小组合作，动手实践。 【学习目标】 1. 掌握利用向量运算解几何题的方法，并能解简单的立体几何问题； 2. 掌握向量运算在几何中求两点间距离和求空间图形中的角度的计算方法. 【重点】利用直线的方向向量及平面的法向量解决空间角的问题. 【难点】利用直线的方向向量及平面的法向量解决空间角的问题. 一、自主学习 1预习教材P105~ P107, 解决下列问题 复习1：已知，，且，求. 复习2:什么叫直线和平面所成角？它的范围是什么？ 复习3：什么叫二面角？二面角的大小如何度量？二面角的范围是什么？ 2. 导学提纲 1. 求出空间线段的长度：用空间向量表示空间线段，然后利用公式_____________. 2. 空间的二面角或异面直线的夹角，都可以转化为利用公式____________求解. 3.空间直线与平面所成角如何转化？试推导出公式：___________________. 4.知识拓展 解空间图形问题时,可以分为三步完成: （1）建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线、平面，把立体几何问题转化为向量问题(还常建立坐标系来辅助)； （2）通过向量运算，研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题； （3）把向量的运算结果“翻译”成相应的几何意义. 二、典型例题 例1.1. 已知，则 . 2. 已知，则的夹角为 . 3. 若M、N分别是棱长为1的正方体的棱的中点,那么直线所成的角的余弦为（ ） A. B. C. D. 4. 将锐角为边长为的菱形沿较短的对角线折成的二面角，则间的距离是（ ） A. B. C. D. 5.正方体中棱长为，,是的中点，则为（ ） A. B. C. D. 例2.如图所示，在长方体中，AB=AD=1，AA1=2，M是棱CC1的中点， （1）求异面直线AB与A1M的夹角 （2）求直线BM与AA1M所成的角 （3）证明：平面ABM与平面A1B1M所成的角(用向量方法) 变式训练：（2010全国卷1理数） 如图，四棱锥S-ABCD中，SD底面ABCD，AB//DC，ADDC，AB=AD=1，DC=SD=2，E为棱SB上的一点，平面EDC平面SBC . （Ⅰ）证明：SE=2EB； （Ⅱ）求二面角A-DE-C的大小 . 例3（2010天津理数） 如图，在长方体中，、分别是棱, 上的点，, （1） 求异面直线与所成角的余弦值； （2） 证明平面 （3） 求二面角的正弦值。 变式训练：（2010浙江文数）如图，在平行四边形ABCD中，AB=2BC，∠ABC=120°。E为线段AB的中点，将△ADE沿直线DE翻折成△A’DE，使平面A’DE⊥平面BCD，F为线段A’C的中点。 （Ⅰ）求证：BF∥平面A’DE； （Ⅱ）设M为线段DE的中点，求直线FM与平面A’DE所成角的余弦值。 三、 变式训练：课本第107页练习2 四、课堂小结 1．知识： 2．数学思想、方法： 3．能力： 四、课后巩固 （1）课本第111页习题1题 （2） 课本第112页A组4题 （3） 课本第112页A组6题 （4） 课本第112页A组10题 （5）处理练习册 4