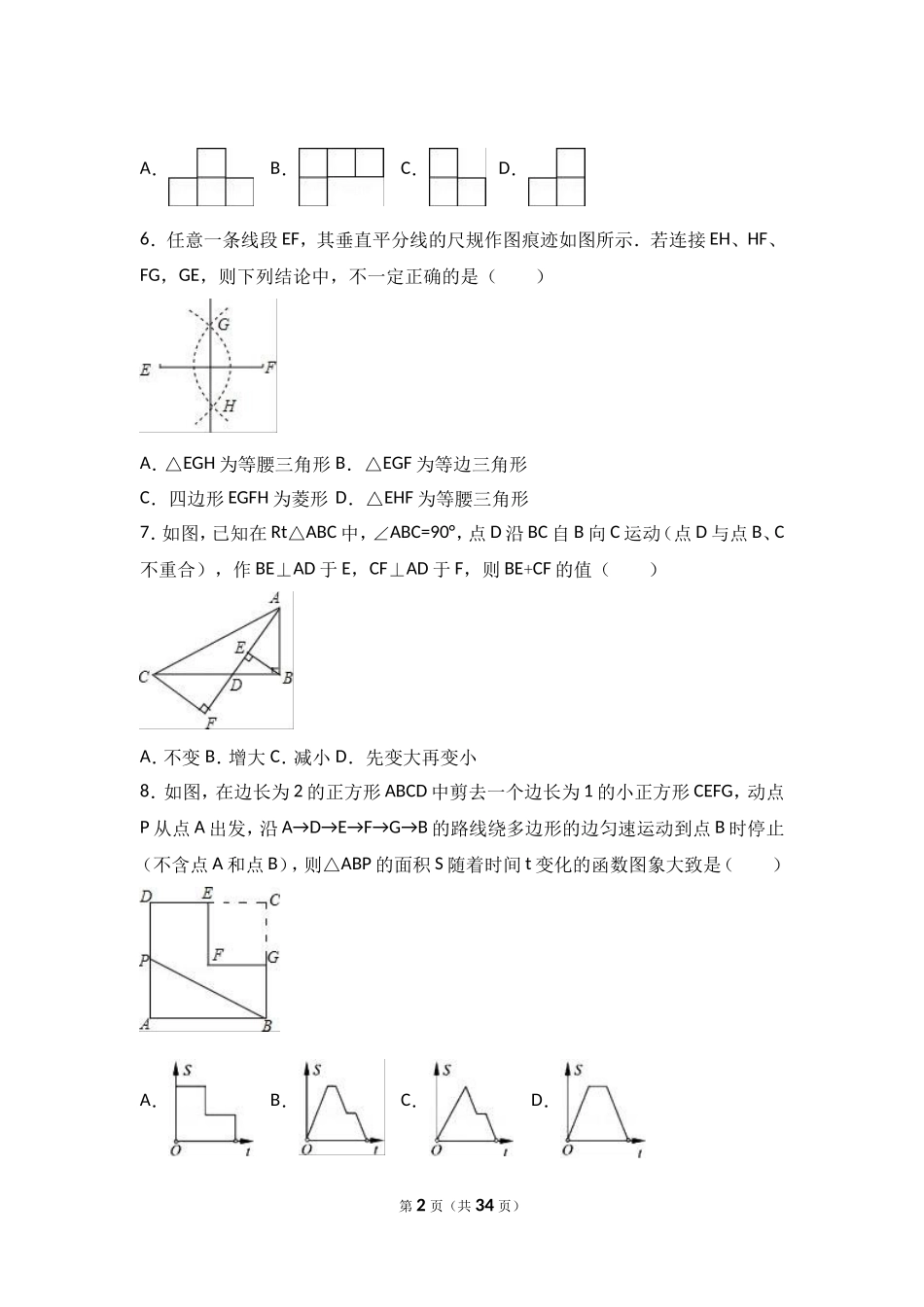
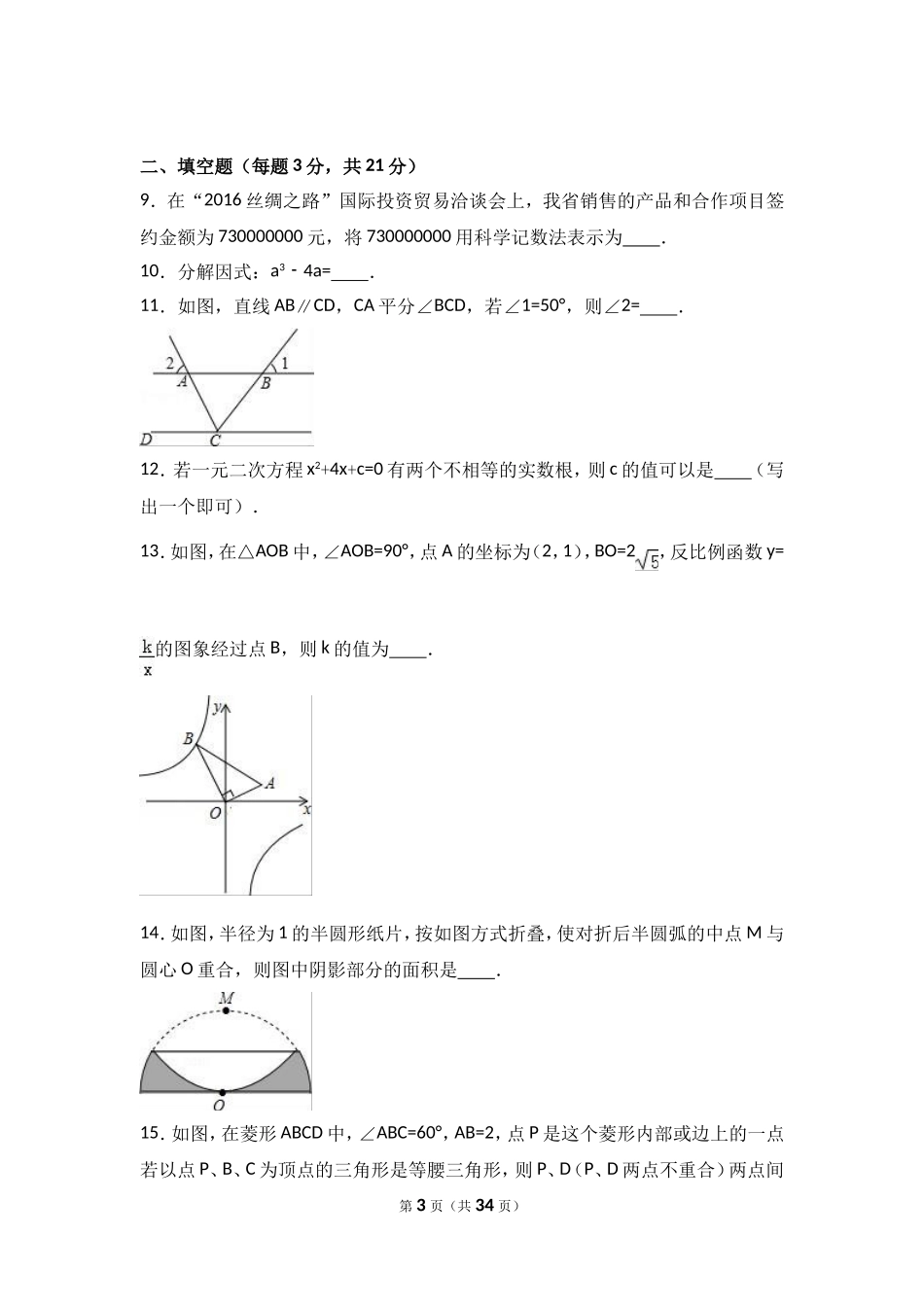
2016-2017学年河南省许昌市长葛市九年级(下)第一次月考数学试卷一、选择题(每题3分,共24分)1.﹣的倒数是()A.2B.﹣2C.D.2.不等式组的解集在数轴上表示正确的是()A.B.C.D.3.在一次数学测试中,某学习小组6名同学的成绩(单位:分)分别为65,82,86,82,76,95.关于这组数据,下列说法错误的是()A.众数是82B.中位数是82C.极差是30D.平均数是824.下列运算正确的是()A.﹣a(ab﹣)=a﹣2ab﹣B.(2ab)2÷a2b=4abC.2ab•3a=6a2bD.(a1﹣)(1a﹣)=a21﹣5.如图是由5个相同的小正方体构成的几何体,其左视图是()第1页(共34页)A.B.C.D.6.任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是()A.△EGH为等腰三角形B.△EGF为等边三角形C.四边形EGFH为菱形D.△EHF为等腰三角形7.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值()A.不变B.增大C.减小D.先变大再变小8.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是()A.B.C.D.第2页(共34页)二、填空题(每题3分,共21分)9.在“2016丝绸之路”国际投资贸易洽谈会上,我省销售的产品和合作项目签约金额为730000000元,将730000000用科学记数法表示为.10.分解因式:a34a=﹣.11.如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=.12.若一元二次方程x2+4x+c=0有两个不相等的实数根,则c的值可以是(写出一个即可).13.如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2,反比例函数y=的图象经过点B,则k的值为.14.如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是.15.如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间第3页(共34页)的最短距离为.三、解答题(共75分)16.先化简:(2x﹣)÷,然后从0,1,﹣2中选择一个适当的数作为x的值代入求值.17.如图,在▱ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.(1)求证:BD∥EF;(2)若=,BE=4,求EC...