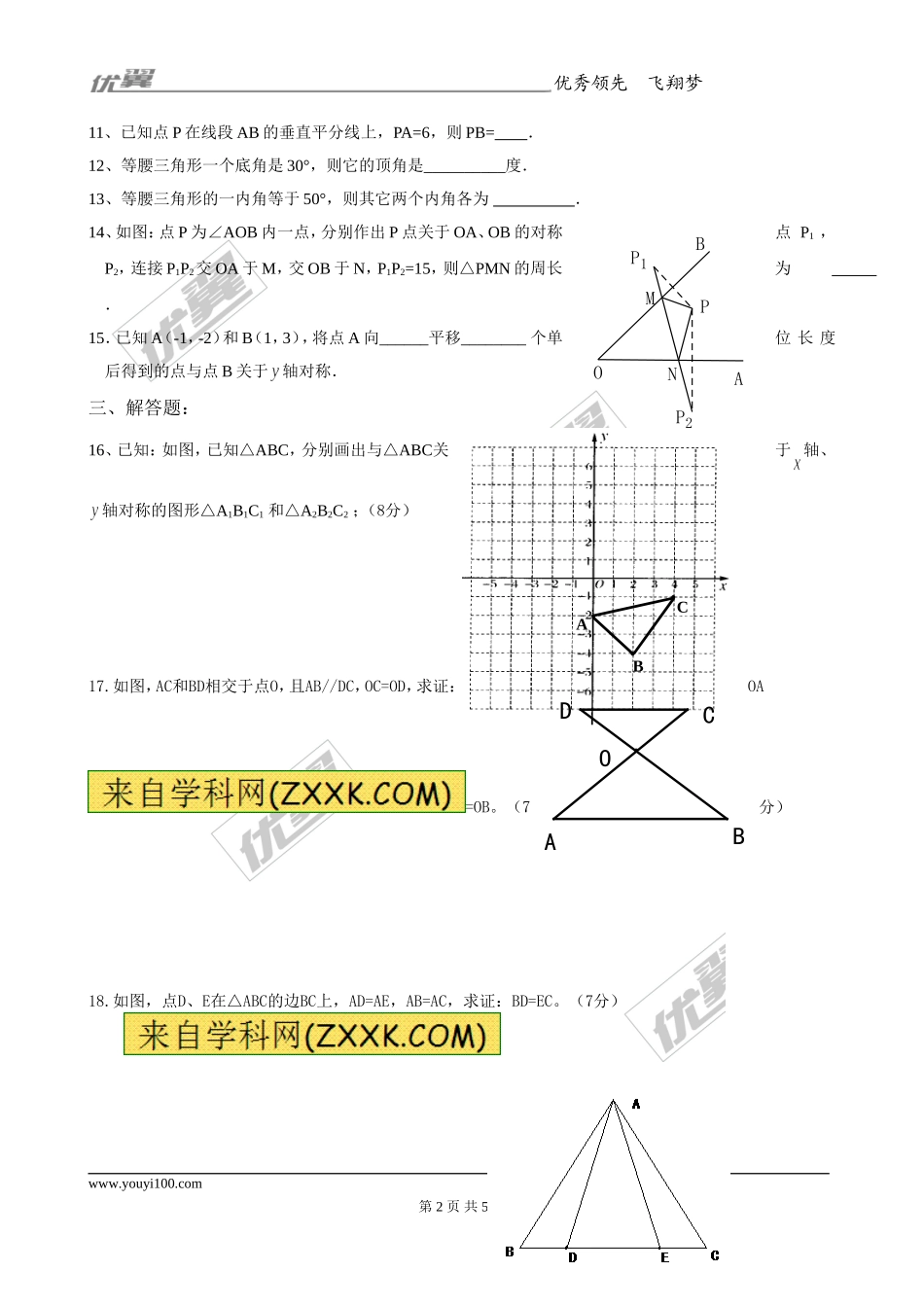
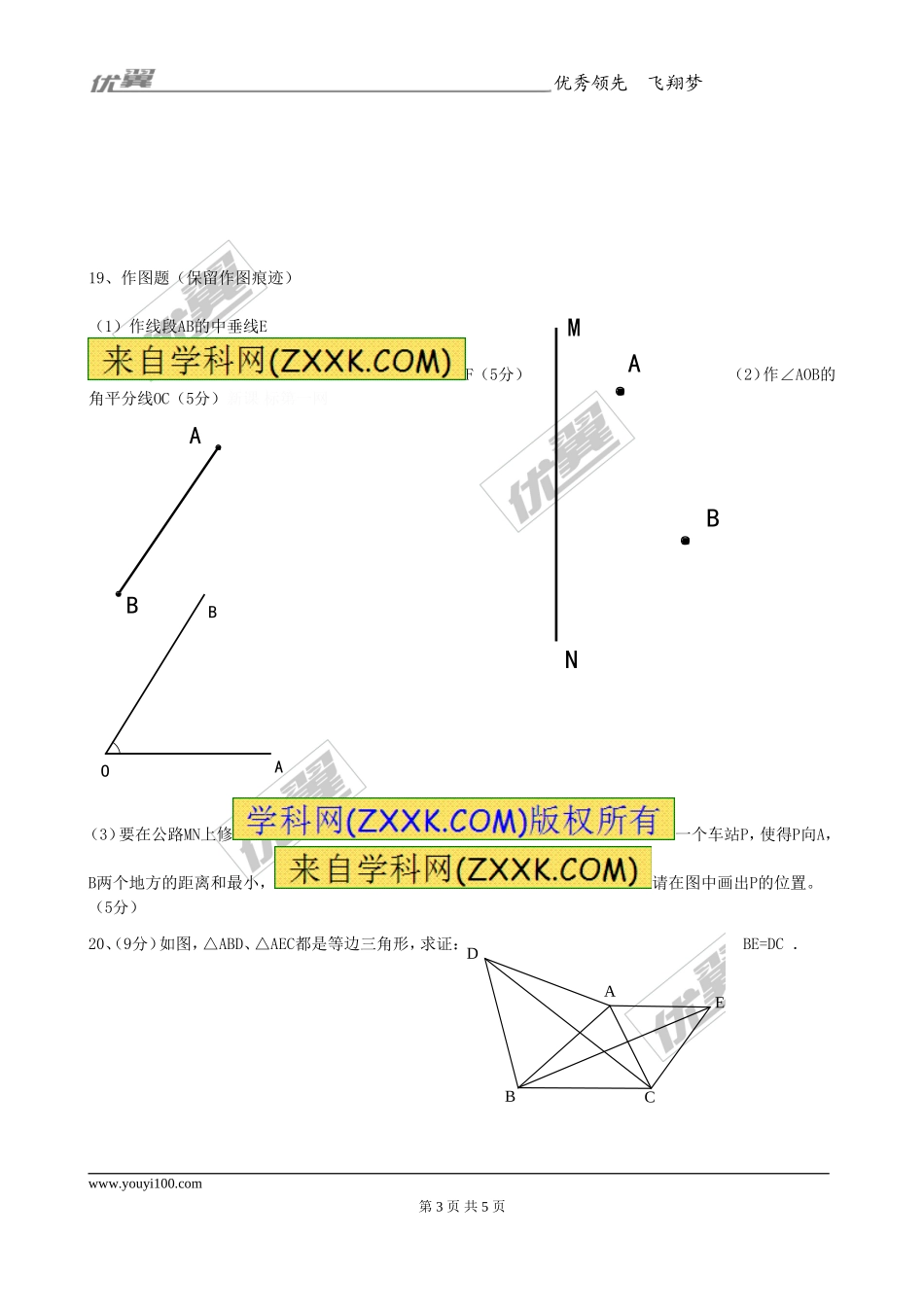
优秀领先飞翔梦想第13章轴对称第Ⅰ卷(选择题共30分)一、选择题(本大题共10题,每小题3分,共30分)1、下列说法正确的是().A.轴对称涉及两个图形,轴对称图形涉及一个图形B.如果两条线段互相垂直平分,那么这两条线段互为对称轴C.所有直角三角形都不是轴对称图形D.有两个内角相等的三角形不是轴对称图形2、点M(1,2)关于轴对称的点的坐标为().A.(-1,-2)B.(-1,2)C.(1,-2)D.(2,-1)3、下列图形中对称轴最多的是().mA.等腰三角形B.正方形C.圆D.线段4、已知直角三角形中30°角所对的直角边为2,则斜边的长为().A.2B.4C.6D.85、若等腰三角形的周长为26,一边为11,则腰长为().A.11B.7.5C.11或7.5D.以上都不对6、如图所示,是四边形ABCD的对称轴,AD∥BC,现给出下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC其中正确的结论有().A.1个B.2个C.3个D.4个7、如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为()厘米.A.16B.18C.26D.288、若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是().A.75°或15°B.75°C.15°D.75°和30°9、等腰三角形ABC在直角坐标系中,底边的两端点坐标是(-2,0),(6,0),则其顶点的坐标,能确定的是().A.横坐标B.纵坐标C.横坐标及纵坐标D.横坐标或纵坐标10、下列图案是几种名车的标志,在这几个图案中不是轴对称图形的是()A:B:C:D:二、填空题(每小题3分,共15分)www.youyi100.com第1页共5页lODCBAEDCBA优秀领先飞翔梦想BCA11、已知点P在线段AB的垂直平分线上,PA=6,则PB=.12、等腰三角形一个底角是30°,则它的顶角是__________度.13、等腰三角形的一内角等于50°,则其它两个内角各为.14、如图:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为.15.已知A(-1,-2)和B(1,3),将点A向______平移________个单位长度后得到的点与点B关于轴对称.三、解答题:16、已知:如图,已知△ABC,分别画出与△ABC关于轴、轴对称的图形△A1B1C1和△A2B2C2;(8分)17.如图,AC和BD相交于点O,且AB//DC,OC=OD,求证:OA=OB。(7分)18.如图,点D、E在△ABC的边BC上,AD=AE,AB=AC,求证:BD=EC。(7分)K[来源:新课|标第|一网ZXX]&网Z&X&www.youyi100.com第2页共5页P2P1NMOPBAOABCD优秀领先飞翔梦想ABCDEX&K]19、作图题(保留作...