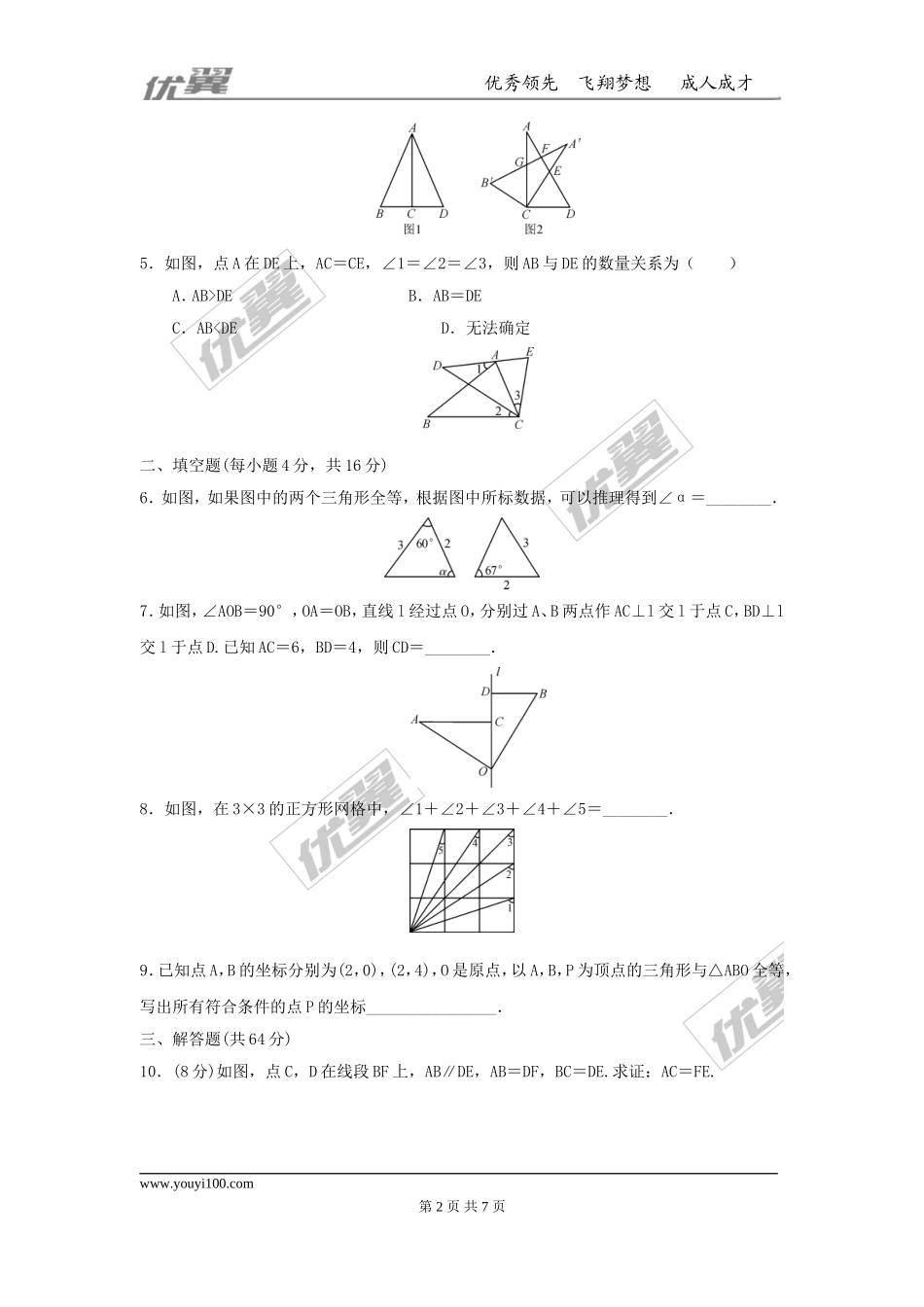
优秀领先飞翔梦想成人成才第十二章全等三角形周周测1一、选择题(每小题4分,共20分)1.下列各组的两个图形属于全等图形的是()2.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为()A.2B.3C.5D.2.53.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E.BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有()A.1组B.2组C.3组D.4组4.(河池中考)如图1,已知两个全等直角三角形的直角顶点及一条直角边重合.将△ACB绕点C按顺时针方向旋转到△A′CB′的位置,其中A′C交直线AD于点E,A′B′分别交直线AD,AC于点F,G,则在图2中,全等三角形共有()21世纪教育网版权所有A.5对B.4对C.3对D.2对www.youyi100.com第1页共7页优秀领先飞翔梦想成人成才5.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则AB与DE的数量关系为()A.AB>DEB.AB=DEC.AB