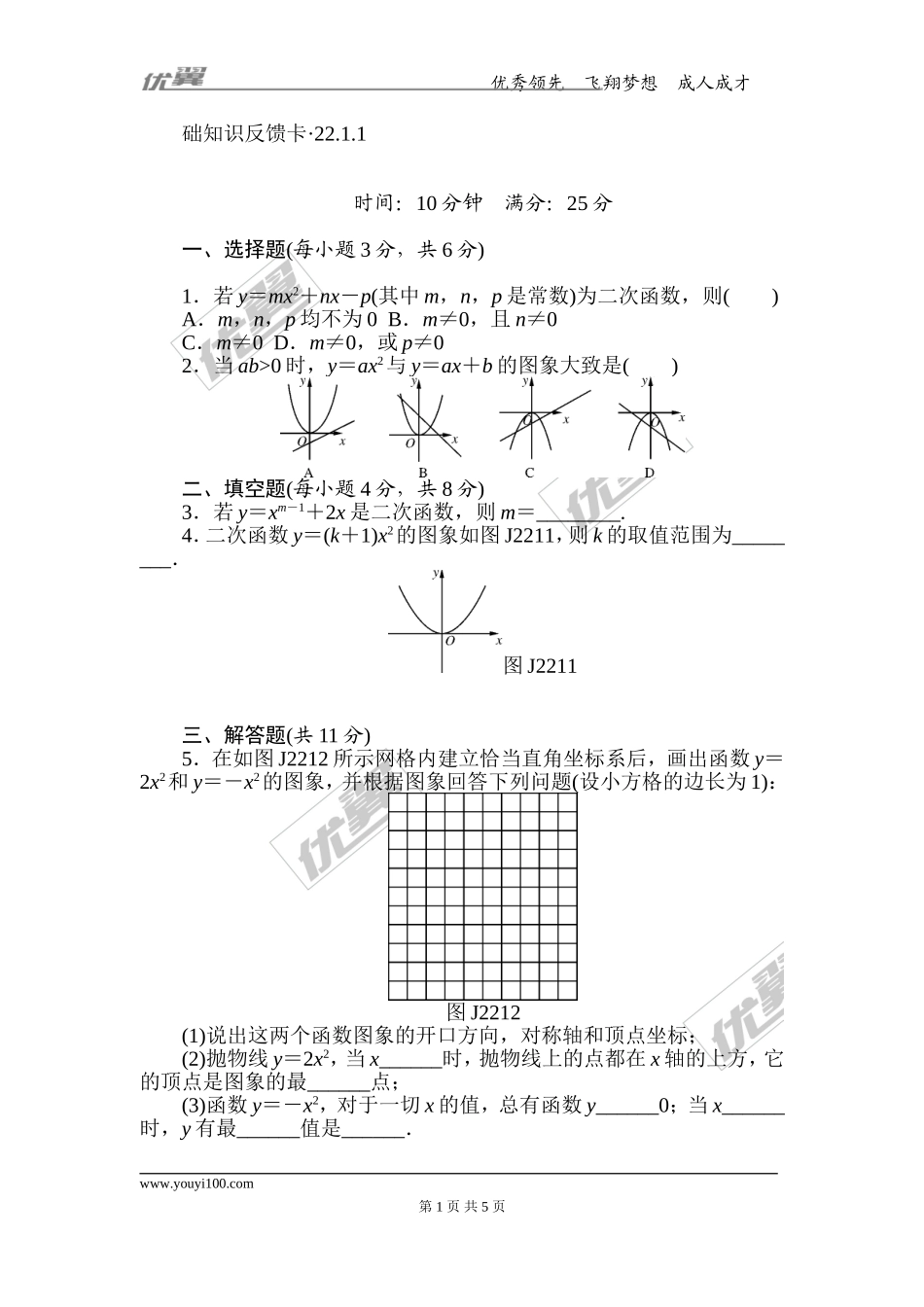
优秀领先飞翔梦想成人成才础知识反馈卡·22.1.1时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.若y=mx2+nx-p(其中m,n,p是常数)为二次函数,则()A.m,n,p均不为0B.m≠0,且n≠0C.m≠0D.m≠0,或p≠02.当ab>0时,y=ax2与y=ax+b的图象大致是()二、填空题(每小题4分,共8分)3.若y=xm-1+2x是二次函数,则m=________.4.二次函数y=(k+1)x2的图象如图J2211,则k的取值范围为________.图J2211三、解答题(共11分)5.在如图J2212所示网格内建立恰当直角坐标系后,画出函数y=2x2和y=-x2的图象,并根据图象回答下列问题(设小方格的边长为1):图J2212(1)说出这两个函数图象的开口方向,对称轴和顶点坐标;(2)抛物线y=2x2,当x______时,抛物线上的点都在x轴的上方,它的顶点是图象的最______点;(3)函数y=-x2,对于一切x的值,总有函数y______0;当x______时,y有最______值是______.www.youyi100.com第1页共5页优秀领先飞翔梦想成人成才基础知识反馈卡·22.1.2时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.下列抛物线的顶点坐标为(0,1)的是()A.y=x2+1B.y=x2-1C.y=(x+1)2D.y=(x-1)22.二次函数y=-x2+2x的图象可能是()二、填空题(每小题4分,共8分)3.抛物线y=x2+的开口向________,对称轴是________.4.将二次函数y=2x2+6x+3化为y=a(x-h)2+k的形式是________.三、解答题(共11分)5.已知二次函数y=-x2+x+4.(1)确定抛物线的开口方向、顶点坐标和对称轴;(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?基础知识反馈卡·*22.1.3时间:10分钟满分:25分一、选择题(每小题3分,共6分)1.已知二次函数的图象过(1,0),(2,0)和(0,2)三点,则该函数的解析式是()A.y=2x2+x+2B.y=x2+3x+2C.y=x2-2x+3D.y=x2-3x+22.若二次函数的图象的顶点坐标为(2,-1),且抛物线过(0,3),则二次函数的解析式是()A.y=-(x-2)2-1B.y=-(x-2)2-1C.y=(x-2)2-1D.y=(x-2)2-1二、填空题(每小题4分,共8分)3.如图J2213,函数y=-(x-h)2+k的图象,则其解析式为____________.图J2213www.youyi100.com第2页共5页优秀领先飞翔梦想成人成才4.已知抛物线y=x2+(m-1)x-的顶点的横坐标是2,则m的值是________.三、解答题(共11分)5.已知当x=1时,二次函数有最大值5,且图象过点(0,-3),求此函数关系式.基础知识反馈卡·22.2时间:10分钟满分:25分一、选...