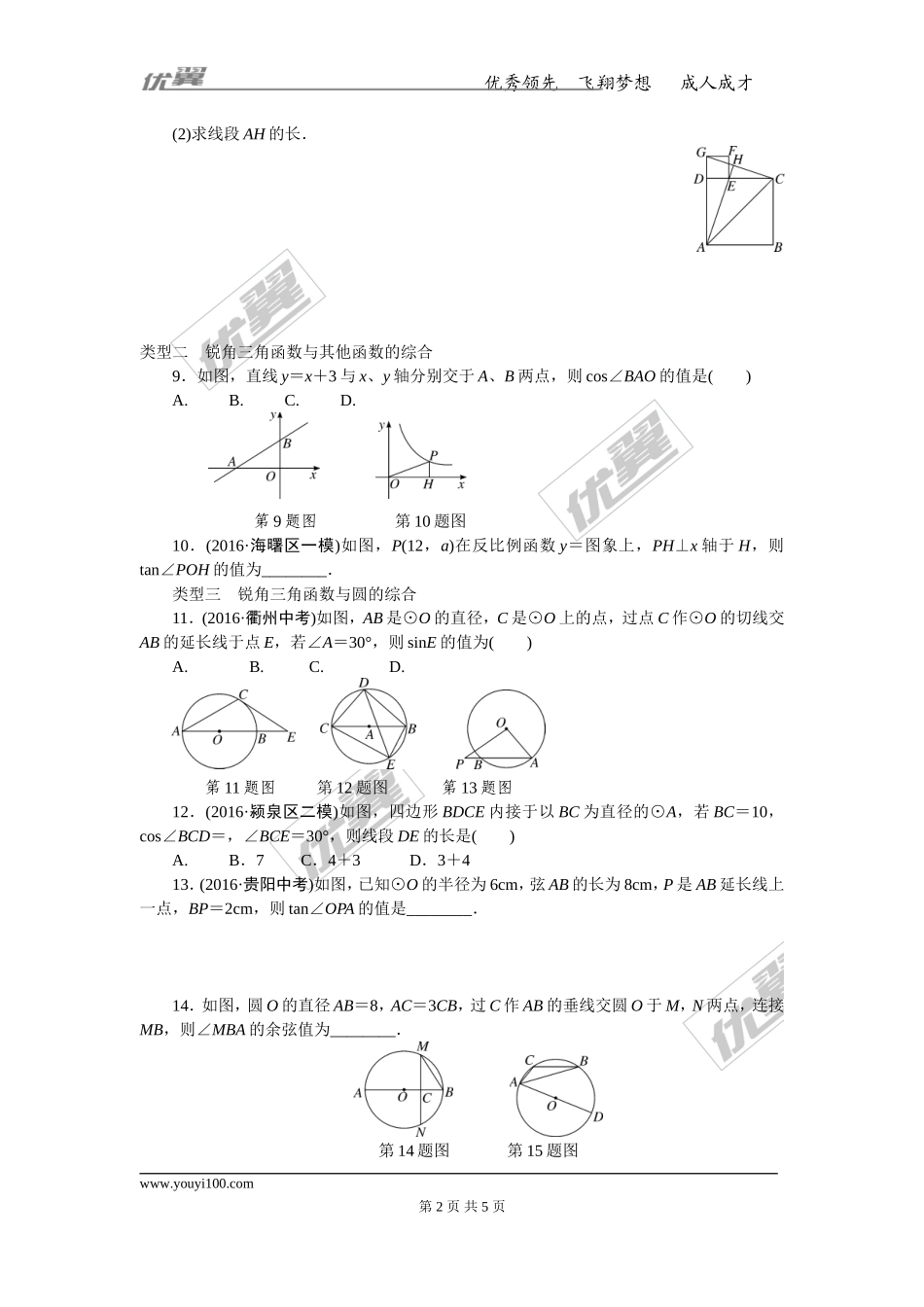
优秀领先飞翔梦想成人成才考点综合专题:锐角三角函数与其他知识的综合——代几结合,掌握中考风向标类型一锐角三角函数与四边形的综合1.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=,AB=4,则AD的长为()A.3B.C.D.第1题图第2题图第3题图2.(2016·宝山区一模)如图,菱形ABCD的边长为10,sin∠BAC=,则对角线AC的长为________.3.(2016·福州中考)如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是________.4.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD=________.第4题图第5题图第6题图5.(2016·菏泽中考)如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.6.(2016·东营中考)如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5cm,且tan∠EFC=,那么矩形ABCD的周长为________cm.7.如图,矩形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD于点E.(1)求证:∠BAM=∠AEF;(2)若AB=4,AD=6,cos∠BAM=,求DE的长.8.(2016·杭州中考)如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.(1)求sin∠EAC的值;www.youyi100.com第1页共5页优秀领先飞翔梦想成人成才(2)求线段AH的长.类型二锐角三角函数与其他函数的综合9.如图,直线y=x+3与x、y轴分别交于A、B两点,则cos∠BAO的值是()A.B.C.D.第9题图第10题图10.(2016·海曙区一模)如图,P(12,a)在反比例函数y=图象上,PH⊥x轴于H,则tan∠POH的值为________.类型三锐角三角函数与圆的综合11.(2016·衢州中考)如图,AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若∠A=30°,则sinE的值为()A.B.C.D.第11题图第12题图第13题图12.(2016·颍泉区二模)如图,四边形BDCE内接于以BC为直径的⊙A,若BC=10,cos∠BCD=,∠BCE=30°,则线段DE的长是()A.B.7C.4+3D.3+413.(2016·贵阳中考)如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是________.14.如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连接MB,则∠MBA的余弦值为________.第14题图第15题图www.youyi100.com第2页共5页优秀领先飞翔梦想成人成才15.如图,⊙O是...