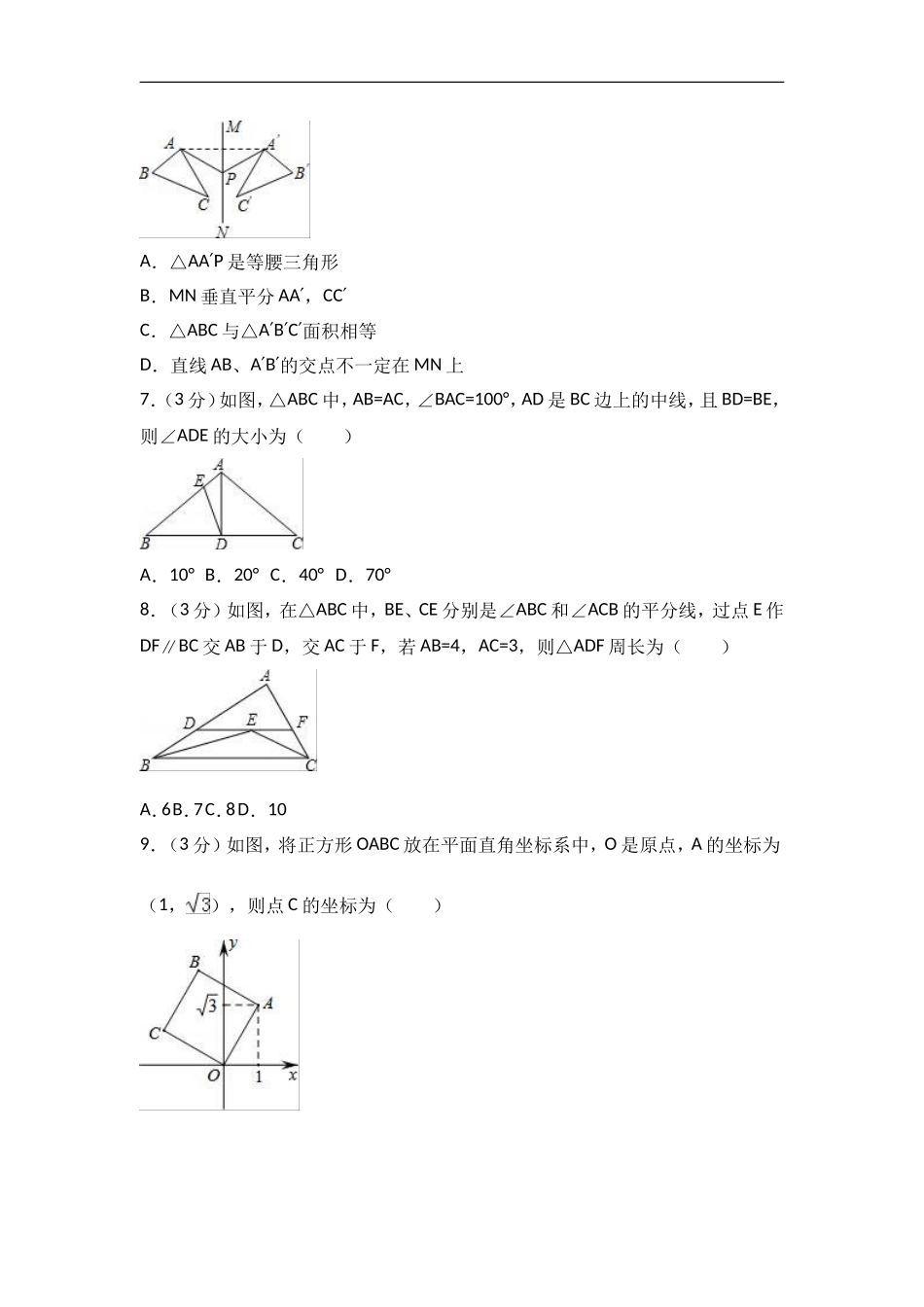
2017-2018学年福建省厦门市五校联考八年级(上)期中数学试卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)在以下回收、绿色食品、节能、节水四个标志中,是轴对称图形的是()A.B.C.D.2.(3分)在平面直角坐标系中,点(3,﹣2)关于y轴对称的点的坐标是()A.(3,2)B.(3,﹣2)C.(﹣3,2)D.(﹣3,﹣2)3.(3分)下列长度的三条线段能组成三角形的是()A.1cm2cm3cmB.6cm2cm3cmC.4cm6cm8cmD.5cm12cm6cm4.(3分)如图,在△ABC中,∠A=55°,∠B=45°,那么∠ACD的度数为()A.110B.100C.55D.455.(3分)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()A.∠A=∠CB.∠D=∠BC.AD∥BCD.DF∥BE6.(3分)如图,△ABC与△ABC′′′关于直线MN对称,P为MN上任一点(P不与AA′共线),下列结论中错误的是()A.△AAP′是等腰三角形B.MN垂直平分AA′,CC′C.△ABC与△ABC′′′面积相等D.直线AB、AB′′的交点不一定在MN上7.(3分)如图,△ABC中,AB=AC,∠BAC=100°,AD是BC边上的中线,且BD=BE,则∠ADE的大小为()A.10°B.20°C.40°D.70°8.(3分)如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB=4,AC=3,则△ADF周长为()A.6B.7C.8D.109.(3分)如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为()A.(﹣,1)B.(﹣1,)C.(,1)D.(﹣,﹣1)10.(3分)已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点所构成的三角形是()A.直角三角形B.钝角三角形C.等腰三角形D.等边三角形二、填空题(共6小题,每小题3分,满分18分)11.(3分)在△ABC中,已知∠A=60°,∠B=80°,则∠C是°.12.(3分)五边形的内角和为.13.(3分)如图,△ABC的边BC的垂直平分线MN交AC于D,若△ADB的周长是10cm,AB=4cm,则AC=cm.[来源:学科网ZXXK]14.(3分)如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是.15.(3分)如图,把长方形纸片ABCD纸沿对角线折叠,若∠BDE=25°,那么∠BED=.16.(3分)如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为.三、解答题(本题共9小题,共86分)17.(8分)...