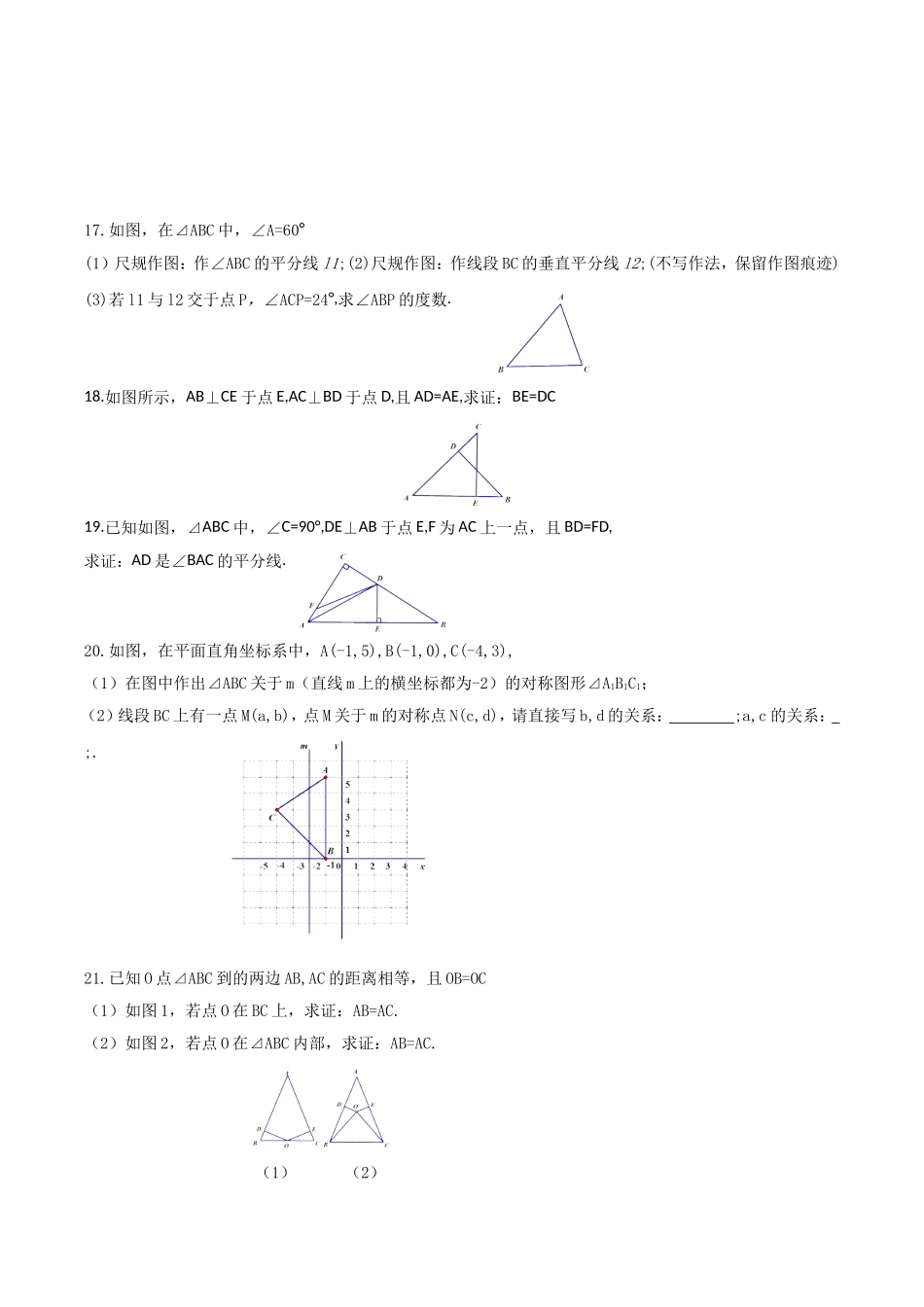
孝感市孝南区2017-2018学年度八年级上学期期中调研考试数学试卷1.下列图形中不是轴对称图形的()2.下列长度的三条线段能组成三角形的是()A.1、2、3;B.1、2、4;C.1、4、3;D.4、2、3;3.一个多边形的内角和是外角和的2倍,则这个多边形的边数为()A.4B.5C.6D.74.如图,⊿ABC与⊿A´B´C´关于l对称,且∠A=105°,∠C´=30°,则∠B为()A.30°B.45°C.55°D.75°5.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定⊿ABC≌⊿ADC的是()A.CB=CD;B.∠BAC=∠DAC;C.∠BCA=∠DCA;D.∠B=∠D=90°;6.已知等腰三角形的底边BC=8cm,且,那么腰AC的长为()A.12cmB.4cmC.12cm或4cmD.以上都不对7.若坐标平面上点P(a,1)与点Q(-4,b)关于x轴对称,则a+b的值为()A.3B.-3C.5D.-58.如图,已知在⊿ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB,AC于点D,E,若BD+CE=5,则线段DE的长为()A.5B.6C.7D.89.如图,在⊿ABC中,∠ACB=90°,∠A=25°,D是AB上一点,将⊿DBC沿CD折叠,使点B落在AC边上的E处,则∠ADE等于()A.25°B.30°C.35°D.40°DBCA10.如图,⊿ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分别是E,F,下列结论:①DE=DF;②D是AC的中点;③DE垂直平分AB;④AB=BC+CD;其中正确的个数为()A.1个B.2个C.3个D.4个11.若点P(m,m-1)在x轴上,则点P关于x轴的对称点为;12.如图,在⊿ABC和⊿EDF中,BD=FC,AB=EF,当添加条件时,就可得到⊿ABC≌⊿EFD.(只需填写一个即可)13.如图所示,在等边⊿ABC中,剪去∠A后,∠1+∠2=;14.如图,BD是∠ABC的平分线,DE⊥AB于E,,AB=18cm,BC=12cm,则DE=;15.如果一个等腰三角形一条腰上的高等于另一腰的一半,则该等腰三角形的顶角的度数为;16.如图,∠AOB=30°,点P为∠AOB内一点,OP=8,点M,N分别在射线OA,OB上,当⊿PMN的周长最小时,下列结论:①∠MPN=120°;②∠MPN=100°;③⊿PMN的周长最小值为24;④⊿PMN的周长最小值为8;其中正确的序号为;17.如图,在⊿ABC中,∠A=60°(1)尺规作图:作∠ABC的平分线l1;(2)尺规作图:作线段BC的垂直平分线l2;(不写作法,保留作图痕迹)(3)若l1与l2交于点P,∠ACP=24°,求∠ABP的度数.18.如图所示,AB⊥CE于点E,AC⊥BD于点D,且AD=AE,求证:BE=DC19.已知如图,⊿ABC中,∠C=90°,DE⊥AB于点E,F为AC上一点,且BD=FD,求证:AD是∠BAC的平分线.20.如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3),(1)在图中作出⊿ABC关于m(直线m上的横坐标都...