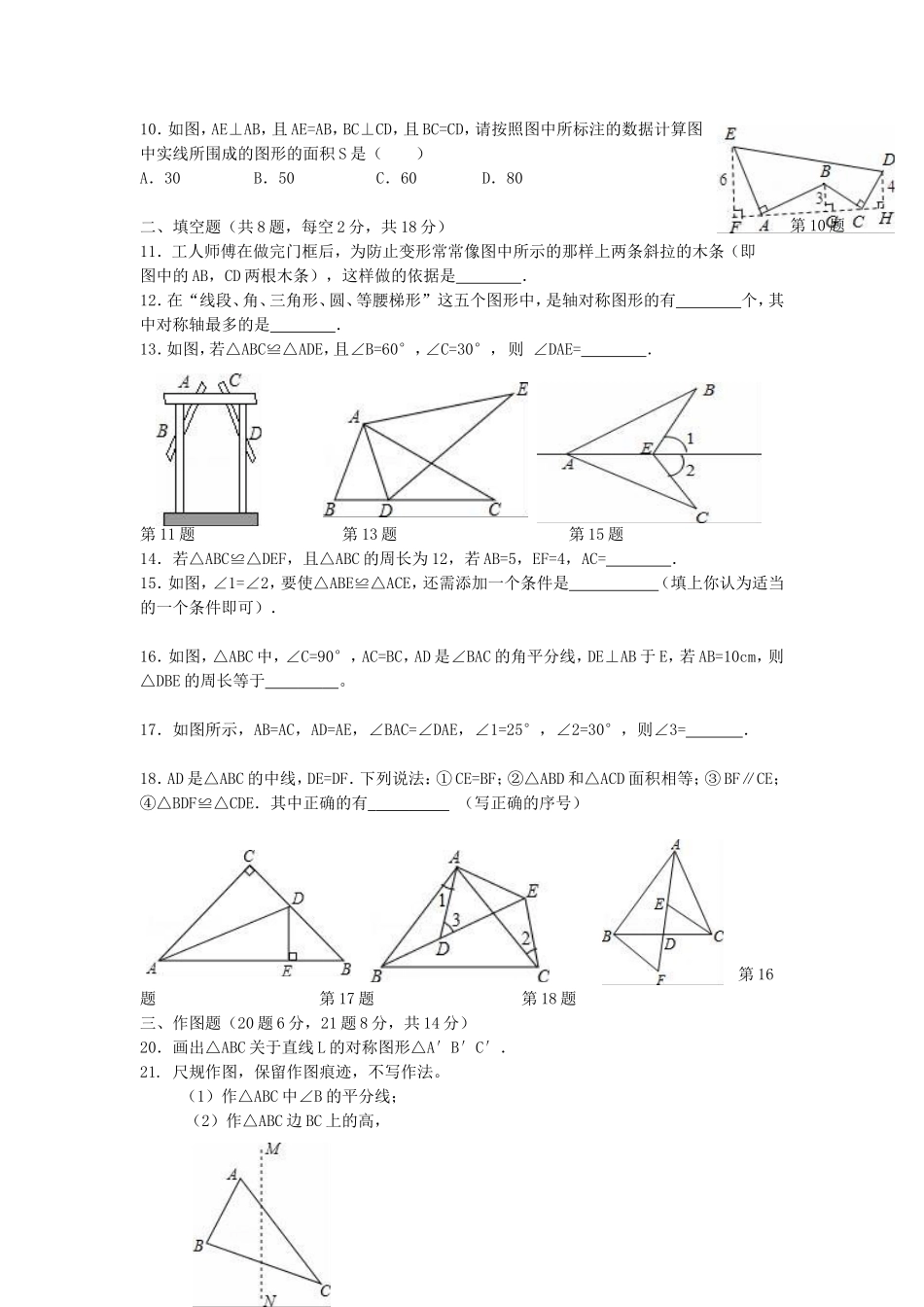
江苏省无锡市宜兴市2017-2018学年八年级数学上学期第一次月考试题考试时间:90分钟满分:100分一、选择题(共10题,每题3分,共30分)1.下面有4个汽车标志图案,其中不是轴对称图形的是()A.B.C.D.2.下列说法正确的是()A.面积相等的两个三角形全等B.周长相等的两个三角形全等C.形状相同的两个三角形全等D.成轴对称的两个三角形全等3、如果两个三角形有两边及一角对应相等,那么这两个三角形()A.一定全等B.一定不全等C.不一定全等D.面积相等4.如图,△ABC与△A′B′C′关于直线l对称,则∠B的度数为()A.30°B.50°C.90°D.100°第4题第5题第6题5.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.∠BAC=∠DACB.CB=CDC.∠BCA=∠DCAD.∠B=∠D=90°6.一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是()A.带其中的任意两块去都可以B.带1、2或2、3去就可以了C.带1、4或3、4去就可以了D.带1、4或2、4或3、4去均可7.如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测BC=5cm,BF=7cm,则BE长为()A.1cmB.2cmC.3cmD.4cm第7题第8题第9题8.如图,是4×4正方形网格,其中已有4个小方格涂成了黑色.现在要从其余白色小方格中选出一个也涂成黑色,使整个黑色部分图形构成轴对称图形,这样的白色小方格有()A.1个B.2个C.3个D.4个9.如图,AB=AC,AC≠BC,AH⊥BC于H,BD⊥AC于D,CE⊥AB于E,AH、BD、CE交于点O,图中全等直角三角形的对数()A.3B.4C.5D.610.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S是()A.30B.50C.60D.80二、填空题(共8题,每空2分,共18分)11.工人师傅在做完门框后,为防止变形常常像图中所示的那样上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是.12.在“线段、角、三角形、圆、等腰梯形”这五个图形中,是轴对称图形的有个,其中对称轴最多的是.13.如图,若△ABC≌△ADE,且∠B=60°,∠C=30°,则∠DAE=.第11题第13题第15题14.若△ABC≌△DEF,且△ABC的周长为12,若AB=5,EF=4,AC=.15.如图,∠1=∠2,要使△ABE≌△ACE,还需添加一个条件是(填上你认为适当的一个条件即可).16.如图,△ABC中,∠...