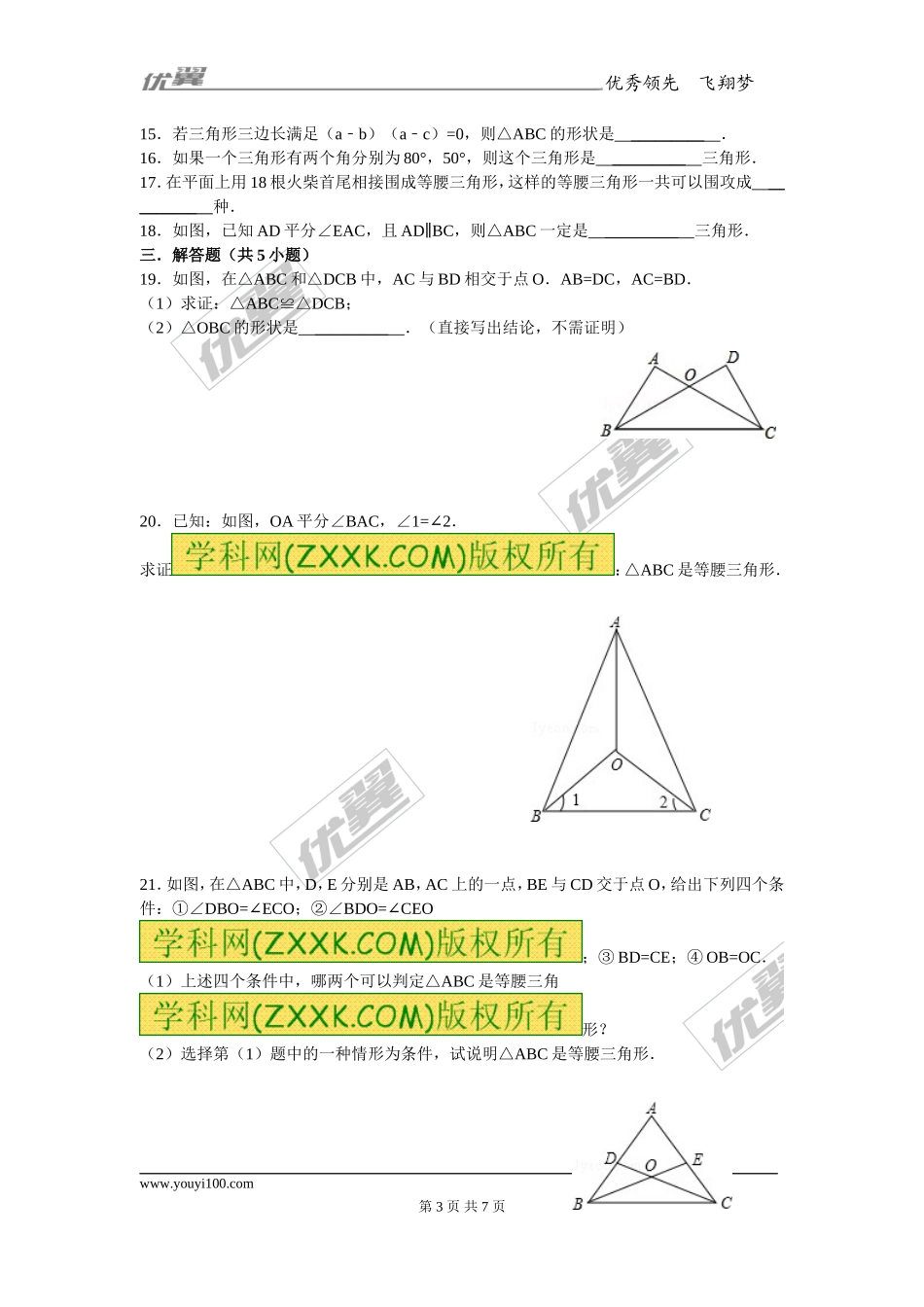
优秀领先飞翔梦想第2课时等腰三角形的判定一.选择题(共8小题)1.如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的角平分线,则图中等腰三角形共有()A.5个B.6个C.7个D.8个第1题第2题第4题7.如图,坐标平面内一点A(2,﹣1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为()A.2B.3C.4D.53.下列条件中不能确定是等腰三角形的是()A.三条边都相等的三角形D.一条中线把面积分成相等的两部分的三角形B.有一个锐角是45°的直角三角形C.一个外角的平分线平行于三角形一边的三角形4.如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=DCO∠;③∠BEO=CDO∠;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有()A.2种B.3种C.4种D.6种5.下列能断定△ABC为等腰三角形的是()A.A=30°∠,∠B=60°B.A=50°∠,∠B=80°C.AB=AC=2,BC=4D.AB=3,BC=7,周长为136.下列说法中:(1)顶角相等,并且有一腰相等的两个等腰三角形全等;(2)底边相等,且周长相等的两个等腰三角形全等;(3)腰长相等,且有一角是50°的两个等腰三角形全等;(4)两条直角边对应相等的两个直角三角形全等;错误的有()A.1个B.2个C.3个D.4个7.已知下列各组数据,可以构成等腰三角形的是()A.1,2,1B.2,2,1C.1,3,1D.2,2,5www.youyi100.com第1页共7页优秀领先飞翔梦想8.已知:如图,下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是()A.①③④B.①②③④C.①②④D.①③二.填空题(共10小题)9.用若干根火柴(不折断)紧接着摆成一个等腰三角形,底边用了10根,则一腰至少要用_________根火柴.10.如图,∠BAC=100°,∠B=40°,∠D=20°,AB=3,则CD=_________第10题第11题第14题第18题11.如图,△ABC是等腰三角形,且AB=AC,BM,CM分别平分∠ABC,∠ACB,DE经过点M,且DEBC∥,则图中有_________个等腰三角形.12.在△ABC中,与∠A相邻的外角是100°,要使△ABC是等腰三角形,则∠B的度数是_________.13.在△ABC中,∠A=100°,当∠B=_________°时,△ABC是等腰三角形.14.如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC,则∠1=_________度,图中有_________个等腰三角形.www.youyi100.com第2页共7页优秀领先飞翔梦想15....