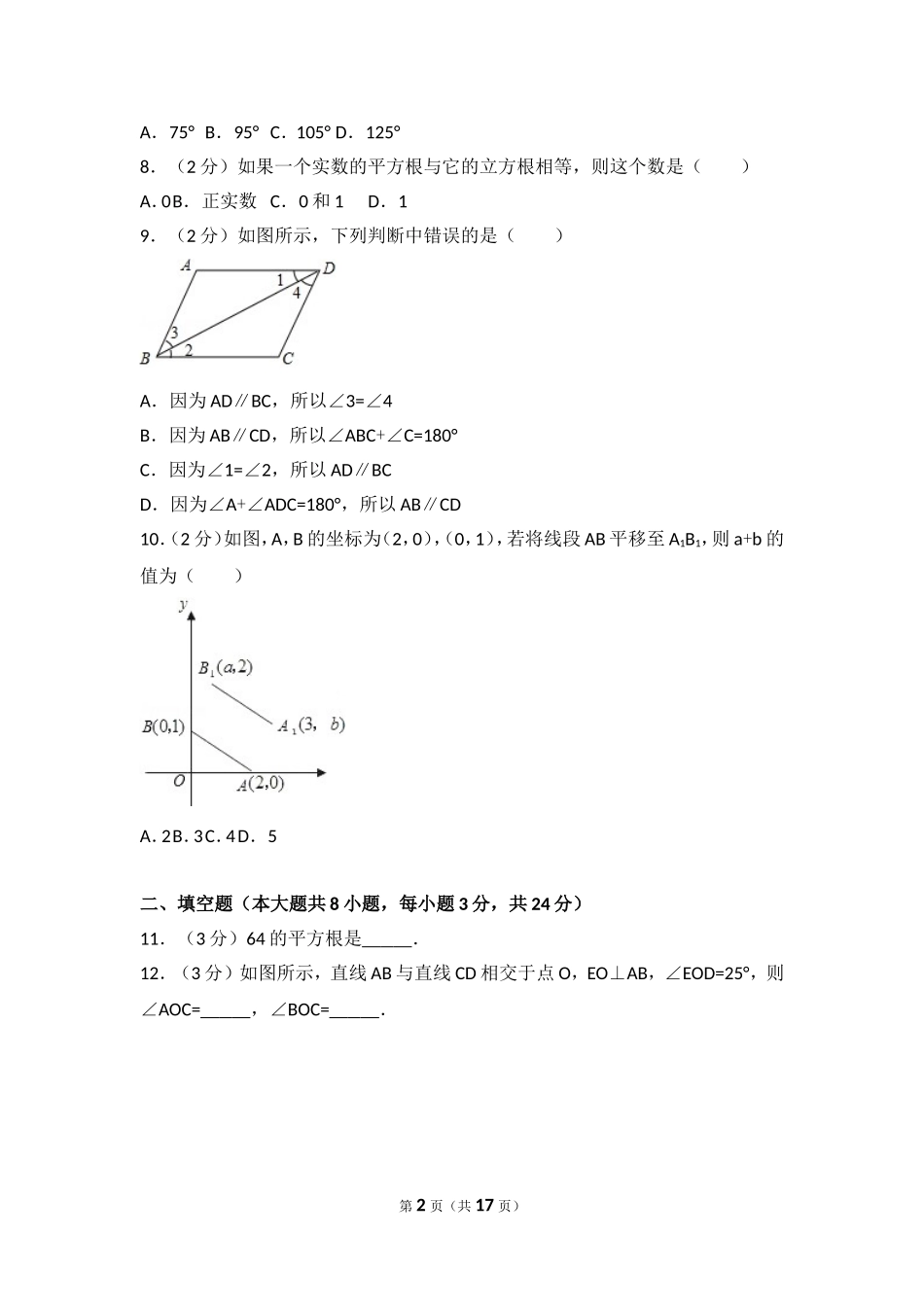
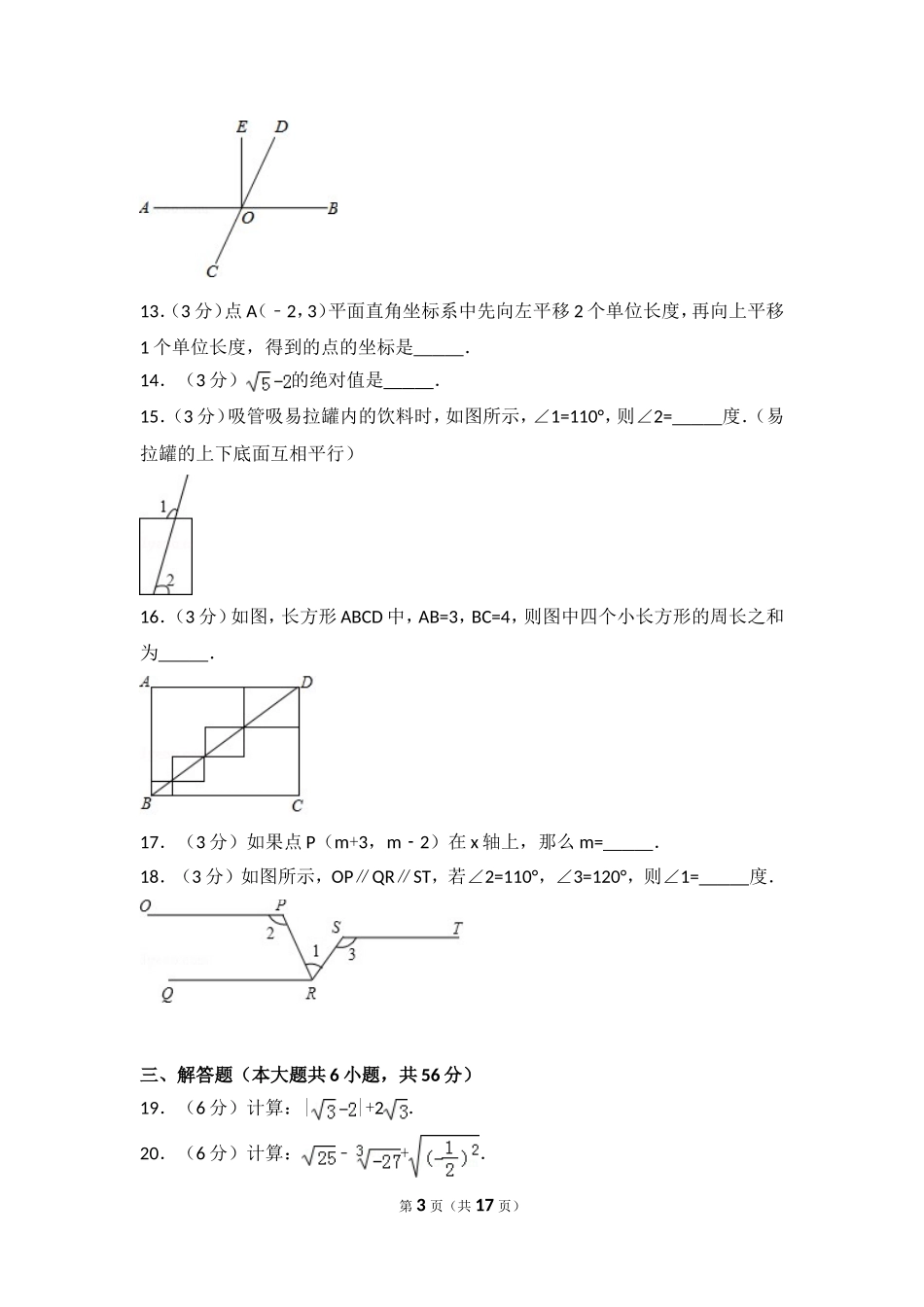
2016-2017学年河北省廊坊市文安县七年级(下)期中数学试卷一、选择题(本大题共10小题,每小题2分,共20分)1.(2分)在平面直角坐标系中,点(﹣2,3)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限2.(2分)下列各组数中互为相反数的是()A.﹣2与B.﹣2与C.2与(﹣)2D.|﹣|与3.(2分)如图所示,下列说法错误的是()A.∠1和∠3是同位角B.∠1和∠5是同位角C.∠1和∠2是同旁内角D.∠5和∠6是内错角4.(2分)已知点P位于y轴右侧,距y轴3个单位长度,位于x轴上方,距离x轴4个单位长度,则点P坐标是()A.(﹣3,4)B.(3,4)C.(﹣4,3)D.(4,3)5.(2分)下列实数属于无理数的是()A.0B.πC.D.﹣6.(2分)下列命题中,真命题的个数有()①对顶角相等;②有一条公共边的两个角叫邻补角;③内错角相等;④在同一平面内,垂直于同一条直线的两直线平行.A.0个B.1个C.2个D.3个7.(2分)如图,一条“U”型水管中AB∥CD,若∠B=75°,则∠C应该等于()第1页(共17页)A.75°B.95°C.105°D.125°8.(2分)如果一个实数的平方根与它的立方根相等,则这个数是()A.0B.正实数C.0和1D.19.(2分)如图所示,下列判断中错误的是()A.因为AD∥BC,所以∠3=∠4B.因为AB∥CD,所以∠ABC+∠C=180°C.因为∠1=∠2,所以AD∥BCD.因为∠A+∠ADC=180°,所以AB∥CD10.(2分)如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2B.3C.4D.5二、填空题(本大题共8小题,每小题3分,共24分)11.(3分)64的平方根是.12.(3分)如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠AOC=,∠BOC=.第2页(共17页)13.(3分)点A(﹣2,3)平面直角坐标系中先向左平移2个单位长度,再向上平移1个单位长度,得到的点的坐标是.14.(3分)的绝对值是.15.(3分)吸管吸易拉罐内的饮料时,如图所示,∠1=110°,则∠2=度.(易拉罐的上下底面互相平行)16.(3分)如图,长方形ABCD中,AB=3,BC=4,则图中四个小长方形的周长之和为.17.(3分)如果点P(m+3,m2﹣)在x轴上,那么m=.18.(3分)如图所示,OP∥QR∥ST,若∠2=110°,∠3=120°,则∠1=度.三、解答题(本大题共6小题,共56分)19.(6分)计算:||+2.20.(6分)计算:﹣+.第3页(共17页)21.(10分)如图,在平面直角坐标系中,一个方格的边长为1个单位长度,三角形MNQ是三角形ABC经...