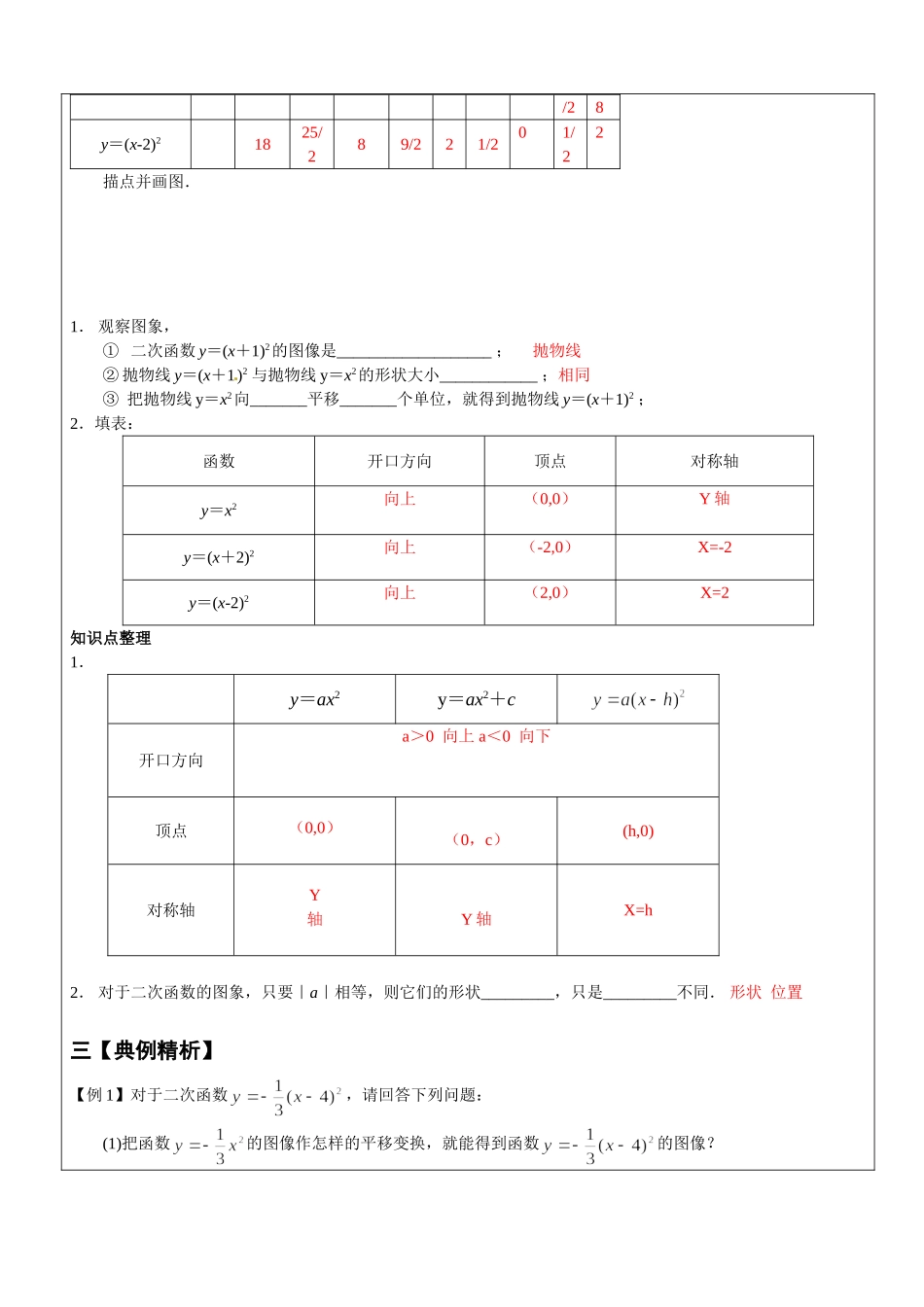
课题二次函数的图像与性质(三)教学目标1.会画二次函数的图象;2.掌握二次函数的性质,并要会灵活应用;重点、难点1.会画二次函数的图象;2.掌握二次函数的性质,并要会灵活应用;考点及考试要求掌握抛物线图像的基本性质(开口方向和大小、对称轴、顶点坐标、增减性和对称性)教学内容一【课堂导入】1、二次函数的图像是什么形状?2、二次函数、、、的性质分别是什么?3、与二者之间的图像有什么关系?平移规律是什么?4、二次函数 a=___2______∴函数有最___小______值。二【知识精讲】知识点1:二次函数的图像画出二次函数y=x2,y=(x+2)2,的图象,并考虑它们的开口方向、对称轴、顶点.先列表:x…-4-3-2-101234y=x2…89/221/201/229/28y=(x+2)2…9/21/201/229/28251-10-8-6-4-2-5-4-3-2-110543218642yOx/28y=(x-2)21825/289/221/201/22描点并画图.1.观察图象,①二次函数y=(x+1)2的图像是___________________;抛物线②抛物线y=(x+1)2与抛物线y=x2的形状大小____________;相同③把抛物线y=x2向_______平移_______个单位,就得到抛物线y=(x+1)2;2.填表:函数开口方向顶点对称轴y=x2向上(0,0)Y轴y=(x+2)2向上(-2,0)X=-2y=(x-2)2向上(2,0)X=2知识点整理1.y=ax2y=ax2+c开口方向a>0向上a<0向下顶点(0,0)(0,c)(h,0)对称轴Y轴Y轴X=h2.对于二次函数的图象,只要|a|相等,则它们的形状_________,只是_________不同.形状位置三【典例精析】【例1】对于二次函数,请回答下列问题:(1)把函数的图像作怎样的平移变换,就能得到函数的图像?(2)说出函数的图像的顶点坐标和对称轴。解:(1)向右平移4个单位(2)顶点坐标:(4,0)对称轴:直线【练习】若把抛物线向左平移2个单位,请写出所得抛物线的解析式及开口方向、顶点坐标、对称轴;若把抛物线向下平移2个单位,请写出所得抛物线的解析式及开口方向、顶点坐标、对称轴.【例2】如图所示,抛物线213(1)yx的顶点为C,与y轴交点为A,过点A作y轴的垂线,交抛物线于另一点B.(1)求直线AC的解析式2ykxb;(2)求△ABC的面积;(3)当自变量x满足什么条件时,有12yy?答案抛物线y=√3(x+1)^2的的顶点为为C(-1,0),与y轴交点为A(0,√3),过A作y轴的垂线:y=√3交抛物线于另一点B(-2,√3),(1)AC的斜率=√3,直线AC的方程是y=√3x+√3.(2)AB=2,C到AB的距离=√3,∴△ABC的面积=√3.【练习】抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,求△AOB的面积和周...