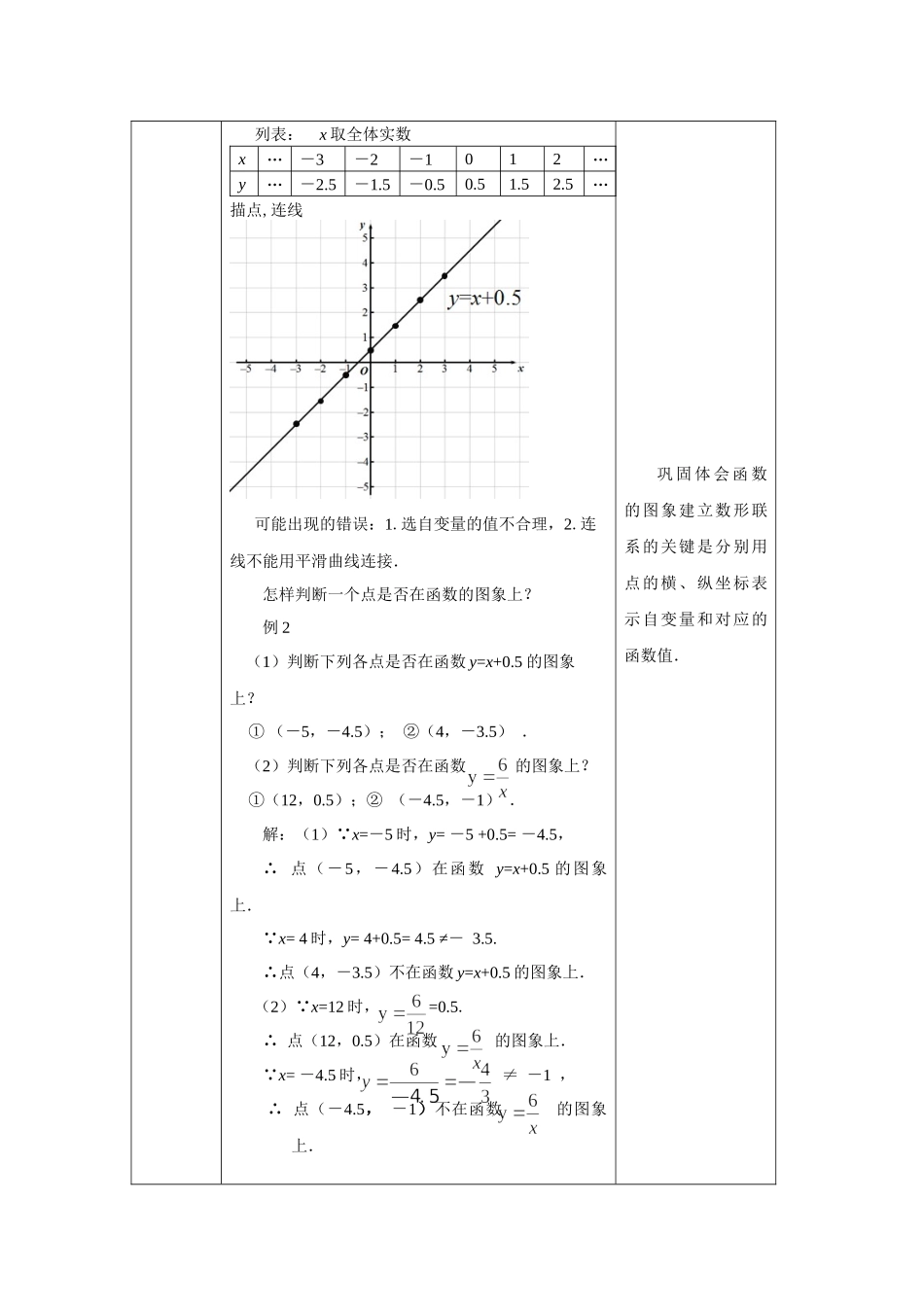
教案教学基本信息课题画函数的图象学科数学学段:初中年级八年级教材书名:数学八年级下册出版社:人民教育出版社出版日期:2013年9月教学设计参与人员姓名单位设计者商立群北京市第三十九中学实施者商立群北京市第三十九中学指导者雷文虹课件制作者商立群北京市第三十九中学其他参与者教学目标及教学重点、难点本节课是在了解函数的图象意义的基础上,进一步学习用描点法画函数的图象.教学目标:1.会用描点法画出函数的图象,能说出画函数的图象的步骤;2.会判断一个点是否在函数的图象上;3.经历画函数的图象的过程,体会函数的图象建立数形联系的关键是分别用点的横、纵坐标表示自变量和对应的函数值.4.能通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合思想.教学重点:描点法画出函数的图象.教学过程(表格描述)教学环节主要教学活动设置意图引入举例说明什么是函数的图象?复习函数的图象概念,为本节课研究画函数的图象做好准备.新课如何画函数的图象?问题:正方形的面积y是边长x的函数,请画出这个函数的图象.结合具体问题,研究画函数的图象的1.思考:(1)这个函数的解析式是什么?(2)这个函数的自变量取值范围是什么?(3)怎样获得组成图象的点?(4)怎样确定满足函数y=x(x>0)的点的坐标?(5)自变量x的一个确定的值与它所对应的函数值y,是否唯一确定一个点(x,y)呢?2.描点法画函数的图象.(1)结合函数的图象的意义研究画法.(2)描点法画函数的图象.①探究画法:②归纳步骤:第一步,列表;第二步,描点;第三步,连线.知识依据.从函数的图象意义出发,思考画函数的图象理论上的操作方法.结合理论上的操作方法的困难,设计研究新的科学方法.总结归纳,形成实践上的画图方法.例题例1在式子y=x+0.5中,对于x每一个确定的值,y有唯一的对应值,即y是x的函数,请画出这个函数的图象.巩固描点法画函数的图象.列表:x取全体实数x…-3-2-1012…y…-2.5-1.5-0.50.51.52.5…描点,连线可能出现的错误:1.选自变量的值不合理,2.连线不能用平滑曲线连接.怎样判断一个点是否在函数的图象上?例2(1)判断下列各点是否在函数y=x+0.5的图象上?①(-5,-4.5);②(4,-3.5).(2)判断下列各点是否在函数的图象上?①(12,0.5);②(-4.5,-1).解:(1) x=-5时,y=-5+0.5=-4.5,∴点(-5,-4.5)在函数y=x+0.5的图象上. x=4时,y=4+0.5=4.5≠-3.5.∴点(4,-3.5)不在...