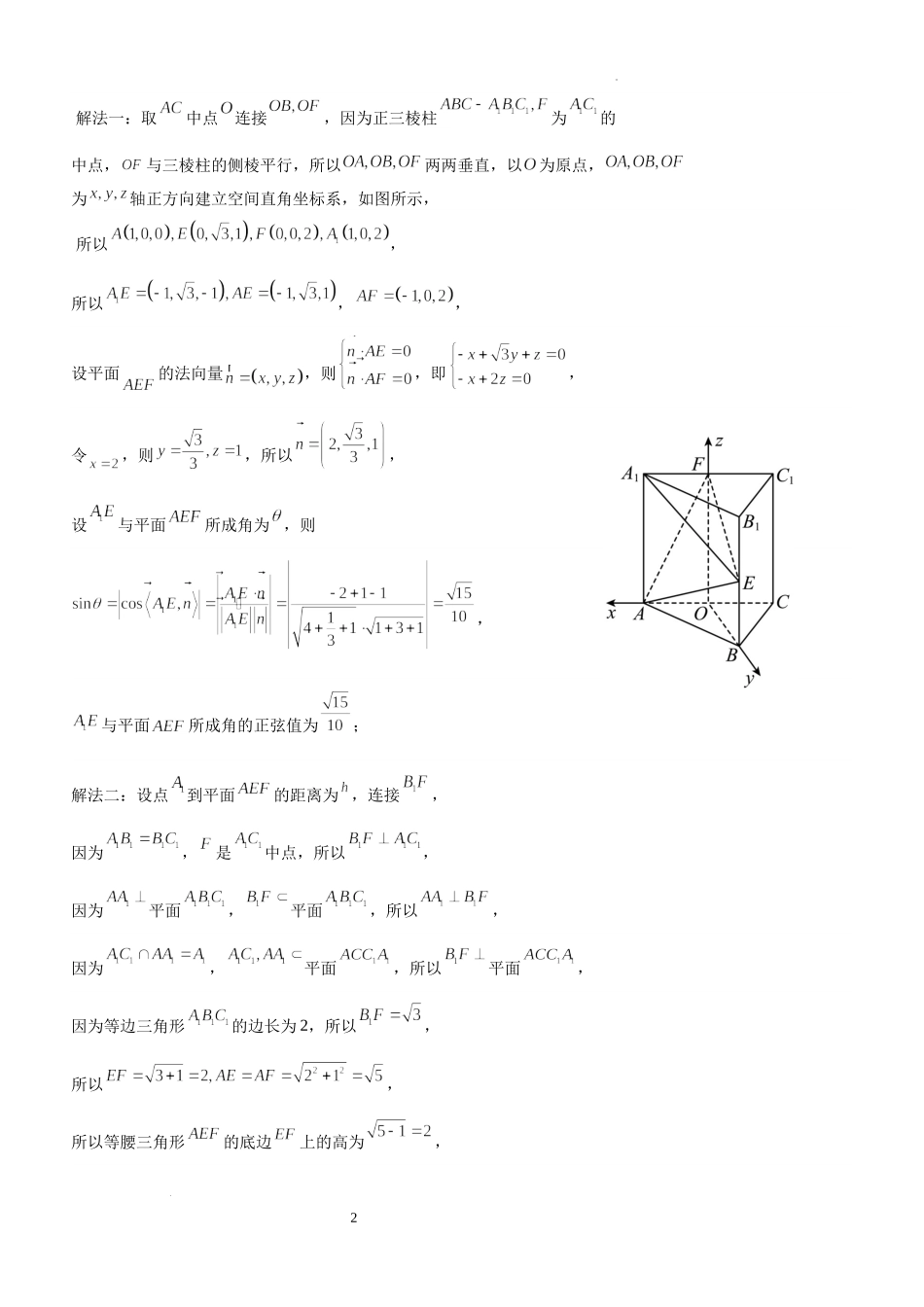
1学科网(北京)股份有限公司泸县五中高2021级高三上学期开学考试理科数学参考答案1.A2.A3.D4.D5.B6.C7.D8.B9.D10.A11.B12.B13.(答案不唯一)14.11015.或或16.17.解:(1)推荐的6名医生中任选3名去参加活动基本事件总数,这6名医生中,外科医生2名,内科医生2名,眼科医生2名,设事件表示“选出的外科医生人数多于内科医生人数”,表示“恰好选出1名外科医生和2名眼科医生”,表示“恰好选出2名外科医生”,,互斥,且,,,选出外科医生人数多于内科医生人数的概率为;(2)由于从6名医生中任选3名的结果为,从6名医生中任选3名,其中恰有名外科医生的结果为,,那么6名中任选3人,恰有名外科医生的概率为,所以,,,.18.解:(1)延长交延长线于点,连接交于点,连接,则过三点的截面就是平面四边形,因为是中点,∥且,所以是的一条中位线,所以∥且,所以;2学科网(北京)股份有限公司解法一:取中点连接,因为正三棱柱为的中点,与三棱柱的侧棱平行,所以两两垂直,以为原点,为轴正方向建立空间直角坐标系,如图所示,所以,所以,,设平面的法向量,则,即,令,则,所以,设与平面所成角为,则,与平面所成角的正弦值为;解法二:设点到平面的距离为,连接,因为,是中点,所以,因为平面,平面,所以,因为,平面,所以平面,因为等边三角形的边长为2,所以,所以,所以等腰三角形的底边上的高为,3学科网(北京)股份有限公司所以的面积为,又的面积为,因为,所以,得,又,设与平面所成角为,则,故平面所成角的正弦值为.19解:(1)由图知:平均数为:;(2)由题设,,则,,,由题意知:,则.20.解:(1)解法一:由,得,又,所以是的极小值点,故,而,故,若,则,当;当,所以在单调递减,在单调递增,故是唯一的极小值点,也是最小值点,由,所以当且仅当时,解法二:由,得,又,当时,有恒成立,所以在上单调递减,又,则不成立,当时,令,得,则时,有时,有,即在单调递减,在单调递增,4学科网(北京)股份有限公司所以的最小值为,,函数在单调递减,单调递增,,当且仅当取等号,故;(2)当时,,设,当时,,又由(1)知,故,当时,,设,则,则在单调递增,,所以,则在单调递增,,综上,,即当时,.21.解:(1)由题意,设,又,则又因为点在圆上,所以,故曲线的方程为;(2)由题意,,设,则,易得斜率必然存在,所以,设,由图象易知,直线斜率不存在时不符合题意设直线的方程为,5...