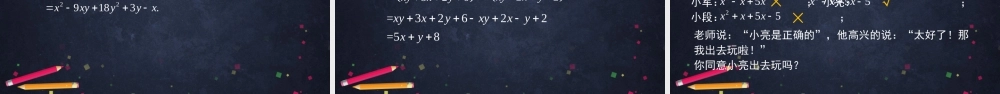【公众号dc008免费分享】0601 -多项式与多项式相乘（第一课时）-2ppt.pptxVIP免费

初一年级数学多项式与多项式相乘(第一课时)北京市通州区马驹桥学校主讲人李亚杰复习计算：2332153xyxy；21124.24xxx复习计算：233253xyxy25解：单×单3x4y32=532xx3yy复习计算：3242.xxx211424xxx解：单×多2=4xx144x142xx++mcba复习在单项式与多项式相乘时，我们利用图形列出代数恒等式.mambmcm(a+b+c)=ma+mb+mc请利用单项式与多项式相乘的法则，进行以下计算.mnabc法1：解：令t=m+n，原式将t=m+n代入上式，上式=(m+n)a+(m+n)b+(m+n)c思考tabc=ma+na+mb+nb+mc+nc；tatbtc=(ma+na)+(mb+nb)+(mc+nc)请利用单项式与多项式相乘的法则，进行以下计算.mnabc法2：解：令s=a+b+c，原式=(m+n)s将s=a+b+c代入，上式=m(a+b+c)+n(a+b+c)思考=ms+ns=ma+mb+mc+na+nb+nc.=(ma+mb+mc)+(na+nb+nc)归纳mnabc=ma+na+mb+nb+mc+nc=ma+mb+mc+na+nb+nc用其中一个多项式的每一项去乘另一个多项式的每一项，再把所得的积相加.=mambmcnanbncnmcbamcba类比用图形解释多项式与多项式乘法的意义.mnabc=m(a+b+c)+n(a+b+c).n(a+b+c)mabcnmbanmcba类比用图形解释多项式与多项式乘法的意义.mnabc(m+n)a+(m+n)b+(m+n)cnma(m+n)a(m+n)b(m+n)c=nmcba解释法则用图形解释多项式与多项式乘法的意义.mancnbnamcmbmnabc=ma+mb+mc+na+nb+nc多×多单×单单×多实践【例】计算：1.(x+3y)(5x+6y)；223.3abaabb；4.32112.xxxx234abab；2.计算(x+3y)(5x+6y)25x2252118xxyy注意1：相乘顺序，严格按照多项式与多项式相乘的法则进行运算.解：问：这是最终结果吗？注意2：检查计算结果是否可以继续合并同类项.5xx6xy35yx36yy6xy218y15xy计算22a222512aabb234abab解：注意3：在运算过程中单项式乘单项式要连带系数的符号一起运算.3ab8ab212b2aa24ab34bb3ba计算223abaabb问：怎样防止丢项漏项？3223aabab322322aababb解：2233ababb计算32112xxxx...