【公众号dc008免费分享】0601 -单项式与多项式相乘-2PPT.pptxVIP免费

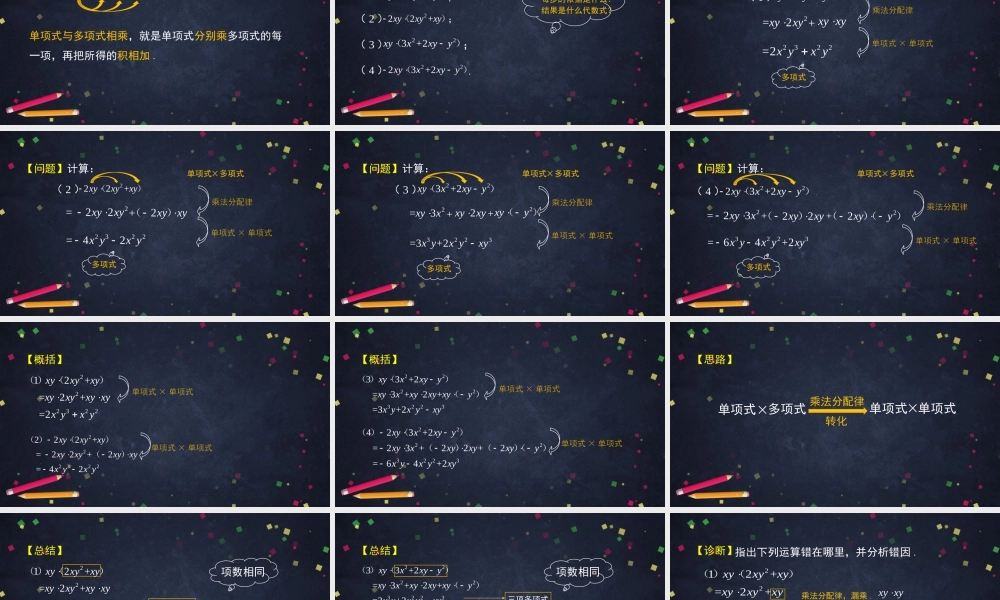
初一年级数学单项式与多项式相乘主讲人王佳菊北京市育才学校通州分校复习：指出下列代数式中的单项式和多项式，其中单项式指出它的系数、字母及字母指数，多项式指出它的各项..2xyxy223+2xxyy22+xyxy、、、.xy2xy、单项式多项式223+2xxyy22+xyxy、单项式系数字母字母指数复习：xy2xy2xyxy11111多项式项复习：22+xyxy23x+2xy2y22xyxy223+2()+xxyy223+2xxyy复习：xy2xy、单项式多项式223+2xxyy22+xyxy、2xyxy（）22+xyxyxy（）223+2xyxxyy（）222+xyxyxy（）2223+2xyxxyy（）2223+22xxyyxyxy（）（）复习：单项式×单项式：2xyxy（）22+xyxyxy（）223+2xyxxyy（）222+xyxyxy（）2223+2xyxxyy（）单项式×多项式：2223+22xxyyxyxy（）（）多项式×多项式：复习：计算:，并叙述单项式与单项式相乘的方法.2xyxy（）222=1(2)=2xyxyxxyyxy（）（）（）系数相乘——积的系数相同字母x的幂相乘相同字母y的幂相乘积的因式22+xyxyxy（）223+2xyxxyy（）222+xyxyxy（）2223+2xyxxyy（）单项式×多项式：复习：++mabc（）引入：++mabc（）=++mambmc乘法对加法的分配律引入：cbam=++mabc（）=++mambmc++=++mabcmambmc（）S1S2S3S大长方形S1+S2+S3=S大长方形长×宽=单项式与多项式相乘，就是单项式分别乘多项式的每一项，再把所得的积相加.总结：++mabc（）=++mambmc【问题】计算：2223+2xyxxyy（）（4）.222+xyxyxy（）（2）；223+2xyxxyy（）；（3）22+xyxyxy（）（1）；如何计算？每步的依据是什么？结果是什么代数式？【问题】计算：22+xyxyxy（）（1）xyxy2322=2xyxy单项式多项式×乘法分配律单项式×单项式多项式2=2xyxy++222+xyxyxy（）（2）【问题】计算：单项式多项式×乘法分配律单项式×单项式多项式2322=42xyxy2xyxy（）2=22xyxy【问题】计算：单项式多项式×乘法分配律单项式×单项式多项式223+2xyxxyy（）（3）2=3xyx3223=3+2xyxyxy2xyy（）2xyxy++【问题】计算：单项式多项式×乘法分配律单项式×单项式多项式2223+2xyxxyy（）（4）3223=64+2xyxyxy2=23xyx22xyxy（）22xyy（）（）++【概括】22232212+=2+=2xyxyxyxyxyxyxyxyxy（）（）222322222+=22+2=42xyxyxyxyxyxyxyxyxy（）（）（）单项式×单项式单...