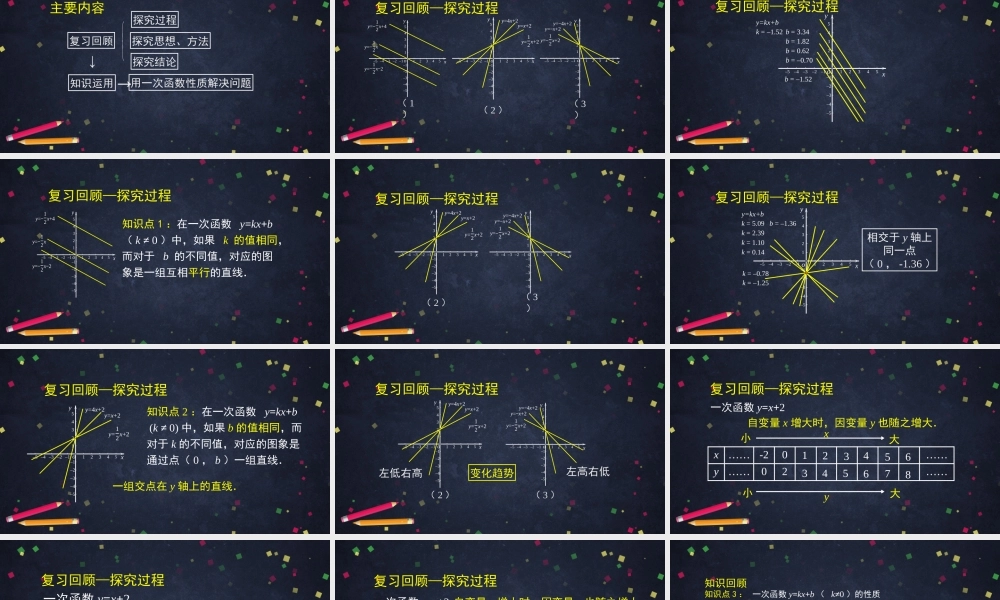
一次函数性质(第二课时)初二年级数学主讲人王轶北京市顺义区第十三中学主要内容探究思想、方法探究结论复习回顾探究过程↓知识运用用一次函数性质解决问题→复习回顾—探究过程yxoy=12x2y=12xy=12x+412345–1–2–3–4–512345–1–2–3–4–5oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5(1)(2)(3)复习回顾—探究过程b=–0.70b=0.62b=1.82b=3.34oyxy=kx+bk=–1.52b=–1.5212345–1–2–3–4–512345–1–2–3–4–5复习回顾—探究过程知识点1:在一次函数y=kx+b(k≠0)中,如果k的值相同,而对于b的不同值,对应的图象是一组互相平行的直线.yxoy=12x2y=12xy=12x+412345–1–2–3–4–512345–1–2–3–4–5复习回顾—探究过程oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5(2)(3)oyxk=–1.25k=–0.78k=0.14k=1.10k=2.39k=5.09y=kx+bb=–1.3612345–1–2–3–4–512345–1–2–3–4–5复习回顾—探究过程相交于y轴上同一点(0,-1.36)复习回顾—探究过程知识点2:在一次函数y=kx+b(k≠0)中,如果b的值相同,而对于k的不同值,对应的图象是通过点(0,b)一组直线.一组交点在y轴上的直线.oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5复习回顾—探究过程oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5oyxy=12x+2y=x+2y=4x+212345–1–2–3–4–512345–1–2–3–4–5(2)(3)左低右高左高右低变化趋势一次函数y=x+2自变量x增大时,因变量y也随之增大.小xx……-20……y……02……大小大132434565678y复习回顾—探究过程一次函数y=x+2y=x+2自变量x增大时,因变量y也随之增大.复习回顾—探究过程y=x+2EE:(2.41,4.41)C:(-1.26,0.74)D:(1.00,3.00)B:(-3.51,-1.51)A:(-4.57,-2.57)DCBAoyx12345–1–2–3–4–512345–1–2–3–4–5大自变量x增大时,因变量y也随之增大.一次函数y=x+2↑小小大↑xy复习回顾—探究过程知识回顾知识点3:一次函数y=kx+b(k≠0)的性质左低右高当k>0时,y随x的增大而增大.xy0k>0知识回顾一次函数y=kx+b(k≠0)的性质左高右低当k<0时,y随x的增大而减小.k<00xy知识回顾—探究思想和方法1.特殊到一般,从几个特例中发现规律,再运用更多特例检验规律的合理性和普遍性,从而得出一般性结论,再...