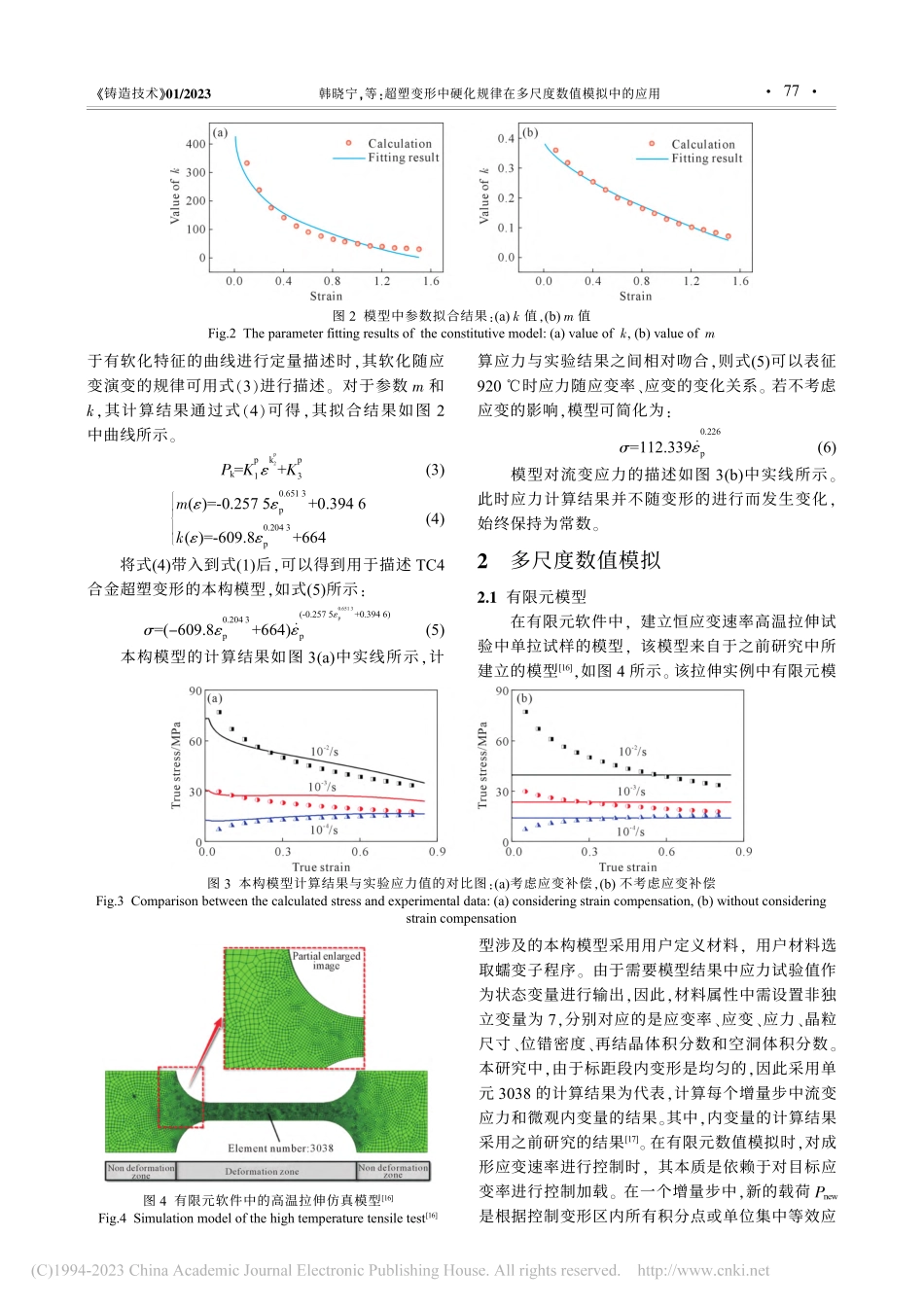
超塑变形中硬化规律在多尺度数值模拟中的应用韩晓宁1,杨俊宙2,吴建军2,李金山1(1.西北工业大学材料学院,陕西西安710072;2.西北工业大学机电学院,陕西西安710072)摘要:为了提高TC4超塑成形多尺度仿真数值模拟的有效性,本文针对高温下材料的硬化规律进行了研究。基于材料流变行为的特点,提出了应变硬化和应变软化的表征模型,并将其应用于超塑成形多尺度数值模拟过程中。研究结果表明,本文所采用的应变补偿模型,可用来描述TC4钛合金在超塑变形中的流变行为。此外,对比晶粒尺度、空洞体积分数等微观尺度变量与多尺度物理本构模型的结果可知,所提出的方案对热变形中微观组织演变的数值模拟是有效的。关键词:超塑变形;数值模拟;应变补偿;本构模型;钛合金中图分类号:TG146.2+3文献标识码:A文章编号:1000-8365(2023)01-0075-05ApplicationoftheHardeningLawintheMultiscaleSimulationforSuperplasticDeformationHANXiaoning1,YANGJunzhou2,WUJianjun2,LIJinshan1(1.SchoolofMaterialsScienceandEngineering,NorthwesternPolytechnicalUniversity,Xi'an710072,China;2.SchoolofMechanicalEngineering,NorthwesternPolytechnicalUniversity,Xi'an710072,China)Abstract:ToimprovetheprecisionofmultiscalenumericalsimulationsforthesuperplasticformationofTC4alloys,thehardeninglawofmetalmaterialsathightemperatureswasinvestigated.Basedontheflowbehaviorofhigh-temperaturetensiletests,asimplemodelconsideringstrainhardeningandsofteningwasproposed.Then,theestablishedmodelwasappliedtothemultiscalenumericalsimulationofsuperplasticforming.TheresultsshowthatthestraincompensationmodelcanbeemployedtodescribetheflowbehaviorofTC4titaniumalloyduringsuperplasticdeformation.Inaddition,comparingthesimulatedresultsofmicroscalevariablessuchasgrainsizeandcavityvolumefractionwiththecalculatedresultsofamultiscalephysicallybasedconstitutivemodel,itcanbeconcludedthattheproposedmethodcouldbeeffectiveforthenumericalsimulationofflowstressesandmicrostructureevolutionduringhotdeformation.Keywords:superplasticdeformation;numericalsimulation;straincompensation;constitutivemodel;titaniumalloy收稿日期:2022-12-02基金项目:国家重点研发计划(2021YFB3702603);国家自然科学基金(52174377...