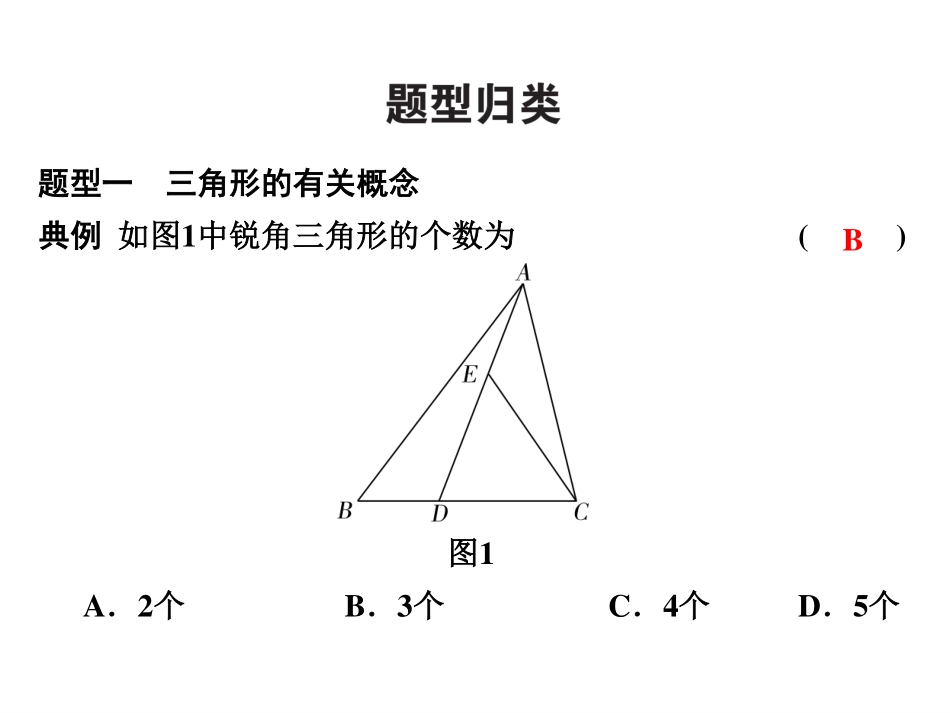
期末高效复习微专题一三角形的初步知识题型一三角形的有关概念典例如图1中锐角三角形的个数为()A.2个B.3个C.4个D.5个图1B【解析】先找出以A为顶点的锐角三角形的个数,再找出以E为顶点的锐角三角形的个数.①以A为顶点的锐角三角形:△ABC,△ADC,共2个;②以E为顶点的锐角三角形:△EDC,共1个,∴图中锐角三角形的个数为2+1=3(个).【点悟】数三角形的个数,可以按照数线段条数的方法,如果一条线段上有n个点,那么就有n(n-1)2条线段,可以与线段外的一点组成n(n-1)2个三角形.变式跟进1.如图2,在△ABC中,AD,BF,CE相交于O点,则图中的三角形的个数是()A.7个B.10个C.15个D.16个D图2【解析】根据三角形的概念,最小的有6个,2个组成一个的有3个,3个组成一个的有6个,最大的有1个,则有6+3+6+1=16(个).题型二三角形的三边关系典例[2018·绥化]三角形三边长分别为3,2a-1,4,则a的取值范围是____________.【点悟】已知三角形的两边长,可根据三边关系确定第三边的取值范围:另外两边之差的绝对值<第三边<另外两边之和.1<a<4变式跟进2.[2017·洛宁期末]三角形的三边长是三个连续的自然数,且三角形的周长小于20,求三边的长.解:设三角形三边的长分别为x-1,x,x+1,则x-1+x>x+1,解得x>2,且x-1+x+x+1<20,解得x<203,∴2<x<203且x为整数,∴x为3,4,5,6,当x=3时,三角形三边为2,3,4;当x=4时,三角形三边为3,4,5;当x=5时,三角形三边为4,5,6;当x=6时,三角形三边为5,6,7.题型三三角形的内角和与外角典例如图3,AD是△ABC的高线,AE是△ABC的角平分线,且∠C=30°,∠B=80°.(1)求∠DAE的度数;(2)请探究∠DAE与∠B,∠C的关系,并说明理由.图3解:(1) ∠BAC+∠B+∠C=180°,∠B=80°,∠C=30°,∴∠BAC=180°-(∠B+∠C)=180°-(80°+30°)=70°,∴∠BAE=12∠BAC=12×70°=35°, AD⊥BC,∴∠B+∠BAD=90°,∴∠BAD=90°-∠B=90°-80°=10°,∴∠DAE=∠BAE-∠BAD=35°-10°=25°;(2)∠DAE=12(∠B-∠C).理由:由(1)可知∠DAE=∠BAE-∠BAD,∠BAE=12∠BAC,∠BAD=90°-∠B,∴∠DAE=12∠BAC-(90°-∠B)=12(180°-∠B-∠C)-(90°-∠B)=12(∠B-∠C).【点悟】(1)三角形的内角和等于180°与三角形的一个外角等于和它不相邻两个内角的和是解决三角形的角度计算的基本依据;(2)由此题得出一个重要的结论:从三角形的一个顶点作...