第1课时相似三角形的性质.pptxVIP免费

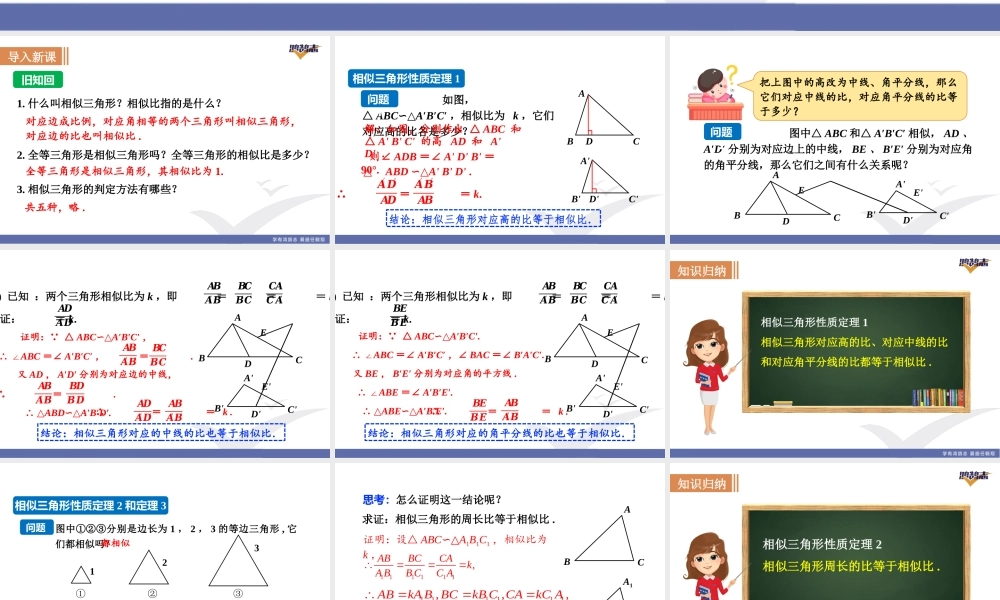
第二十二章相似形22.3相似三角形的性质第1课时相似三角形的性质导入新课旧知回顾1.什么叫相似三角形？相似比指的是什么？2.全等三角形是相似三角形吗？全等三角形的相似比是多少？3.相似三角形的判定方法有哪些？对应边成比例，对应角相等的两个三角形叫相似三角形，对应边的比也叫相似比.全等三角形是相似三角形，其相似比为1.共五种，略.如图，△ABC∽△A′B′C′，相似比为k，它们对应高的比各是多少？相似三角形性质定理1问题1解：如图，分别作出△ABC和△A'B'C'的高AD和A'D'．则∠ADB＝∠A'D'B'＝90°.△ABD∽△A'B'D'.A'B'C'D'ABCD结论：相似三角形对应高的比等于相似比．∴＝＝k.𝑨′𝑫′𝑨𝑫𝑨′𝑩′𝑨𝑩图中△ABC和△A′B′C′相似，AD、A′D′分别为对应边上的中线，BE、B′E′分别为对应角的角平分线，那么它们之间有什么关系呢？ABCDEA'B'D'C'E'问题2把上图中的高改为中线、角平分线，那么它们对应中线的比，对应角平分线的比等于多少？结论：相似三角形对应的中线的比也等于相似比．)已知：两个三角形相似比为k，即＝＝＝k证：＝k.𝑨𝑩𝑨′𝑩′𝑩𝑪𝑩′𝑪′𝑪𝑨𝑪′𝑨′𝑨𝑫𝑨′𝑫′证明： △ABC∽△A′B′C′，∴∠ABC＝∠A′B′C′，＝.𝑨𝑩𝑨′𝑩′𝑩𝑪𝑩′𝑪′又AD，A′D′分别为对应边的中线，∴＝.𝑨𝑩𝑨′𝑩′𝑩𝑫𝑩′𝑫′∴△ABD∽△A′B′D′.ABCDEA'B'D'C'E'∴＝＝k.𝑨𝑫𝑨′𝑫′𝑨𝑩𝑨′𝑩′结论：相似三角形对应的角平分线的比也等于相似比．)已知：两个三角形相似比为k，即＝＝＝k证：＝k.𝑨𝑩𝑨′𝑩′𝑩𝑪𝑩′𝑪′𝑪𝑨𝑪′𝑨′𝑩𝑬𝑩′𝑬′证明： △ABC∽△A′B′C′.∴∠ABC＝∠A′B′C′，∠BAC＝∠B′A′C′.又BE，B′E′分别为对应角的平方线.∴△ABE∽△A′B′E′.ABCDEA'B'D'C'E'∴∠ABE＝∠A′B′E′.∴＝＝k.𝑩𝑬𝑩′𝑬′𝑨𝑩𝑨′𝑩′知识归纳相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.图中①②③分别是边长为1，2，3的等边三角形,它们都相似吗？①1②2③3①与②的相似比＝______，①与②的周长比＝______；①与③的相似比＝______，①与③的周长比＝______.1:2都相似相似三角形性质定理2和定理3问题31:21:31:3结论：相似三角形的周长比等于相似比．证明：设△ABC∽△A1B1C1，相似比为k，111111,ABBCCAkABBCCA111111,,,ABkABBCkBCCAkCA111111111111111111.ABBCCAkABkBCkCAkABBCCAABBCCA有求证：相似三角形的周长比等于相似...