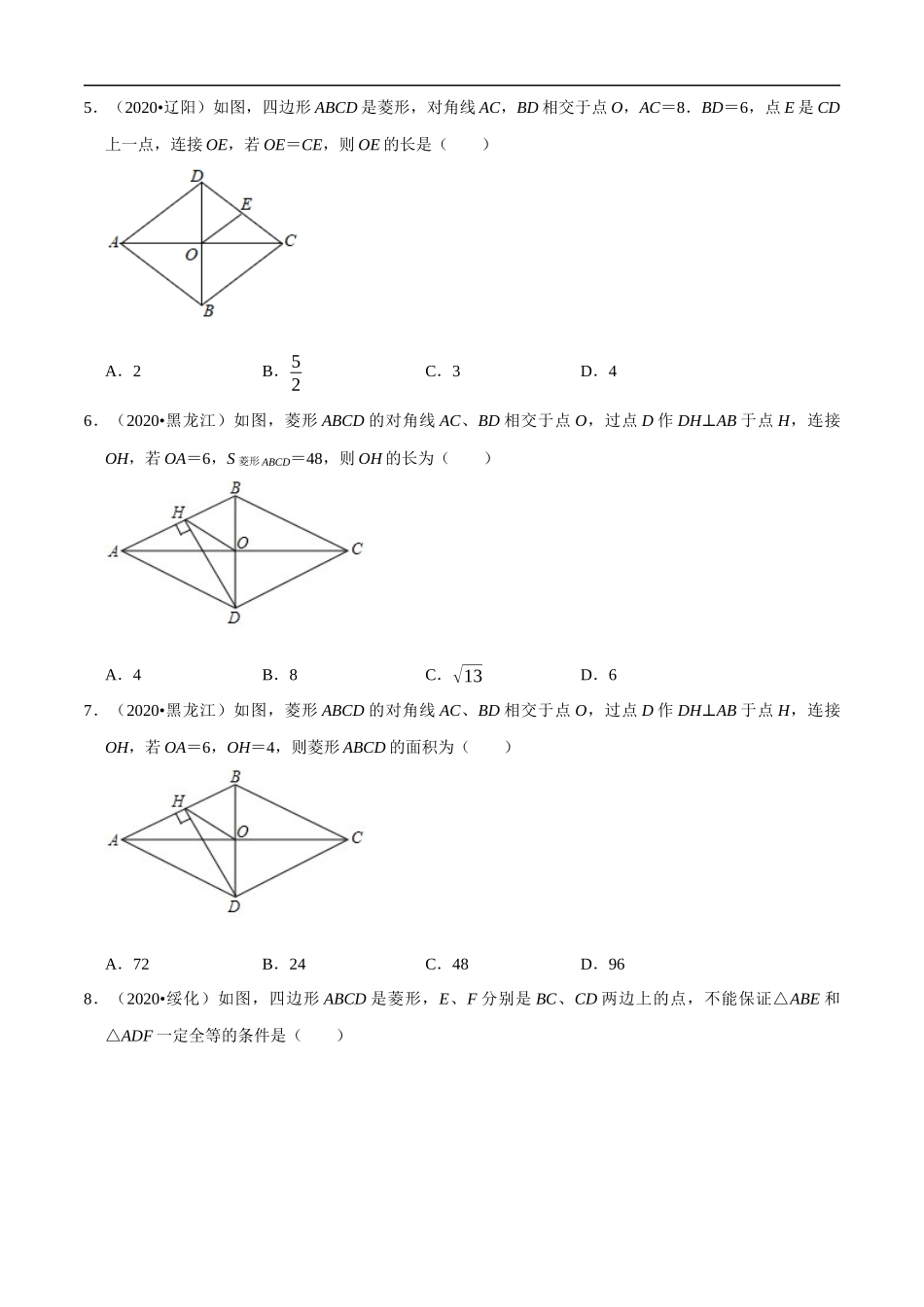
2020年中考数学真题分项汇编(全国通用)专题16矩形菱形正方形一.选择题(共24小题)1.(2020•荆门)如图,菱形ABCD中,E,F分别是AD,BD的中点,若EF=5,则菱形ABCD的周长为()A.20B.30C.40D.502.(2020•黄冈)若菱形的周长为16,高为2,则菱形两邻角的度数之比为()A.4:1B.5:1C.6:1D.7:13.(2020•牡丹江)如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,AD∥x轴且AD=4,∠A=60°,将菱形ABCD绕点O旋转,使点D落在x轴上,则旋转后点C的对应点的坐标是()A.(0,2√3)B.(2,﹣4)C.(2√3,0)D.(0,2√3)或(0,﹣2√3)4.(2020•盐城)如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为()A.125B.52C.3D.55.(2020•辽阳)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是()A.2B.52C.3D.46.(2020•黑龙江)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为()A.4B.8C.√13D.67.(2020•黑龙江)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为()A.72B.24C.48D.968.(2020•绥化)如图,四边形ABCD是菱形,E、F分别是BC、CD两边上的点,不能保证△ABE和△ADF一定全等的条件是()A.∠BAF=∠DAEB.EC=FCC.AE=AFD.BE=DF9.(2020•乐山)如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于点E,连结OA.则四边形AOED的周长为()A.9+2√3B.9+√3C.7+2√3D.810.(2020•甘孜州)如图,菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点.若菱形ABCD的周长为32,则OE的长为()A.3B.4C.5D.611.(2020•贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是()A.5B.20C.24D.3212.(2020•南充)如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC的中点,过点E作EF⊥BD于F,EG⊥AC于G,则四边形EFOG的面积为()A.14SB.18SC.112SD.116S13.(2020•遵义)如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为()A.125B.185C.4D.24514.(2020•湘西州)如图,在平面直角坐标系xOy中,矩形ABCD的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半...