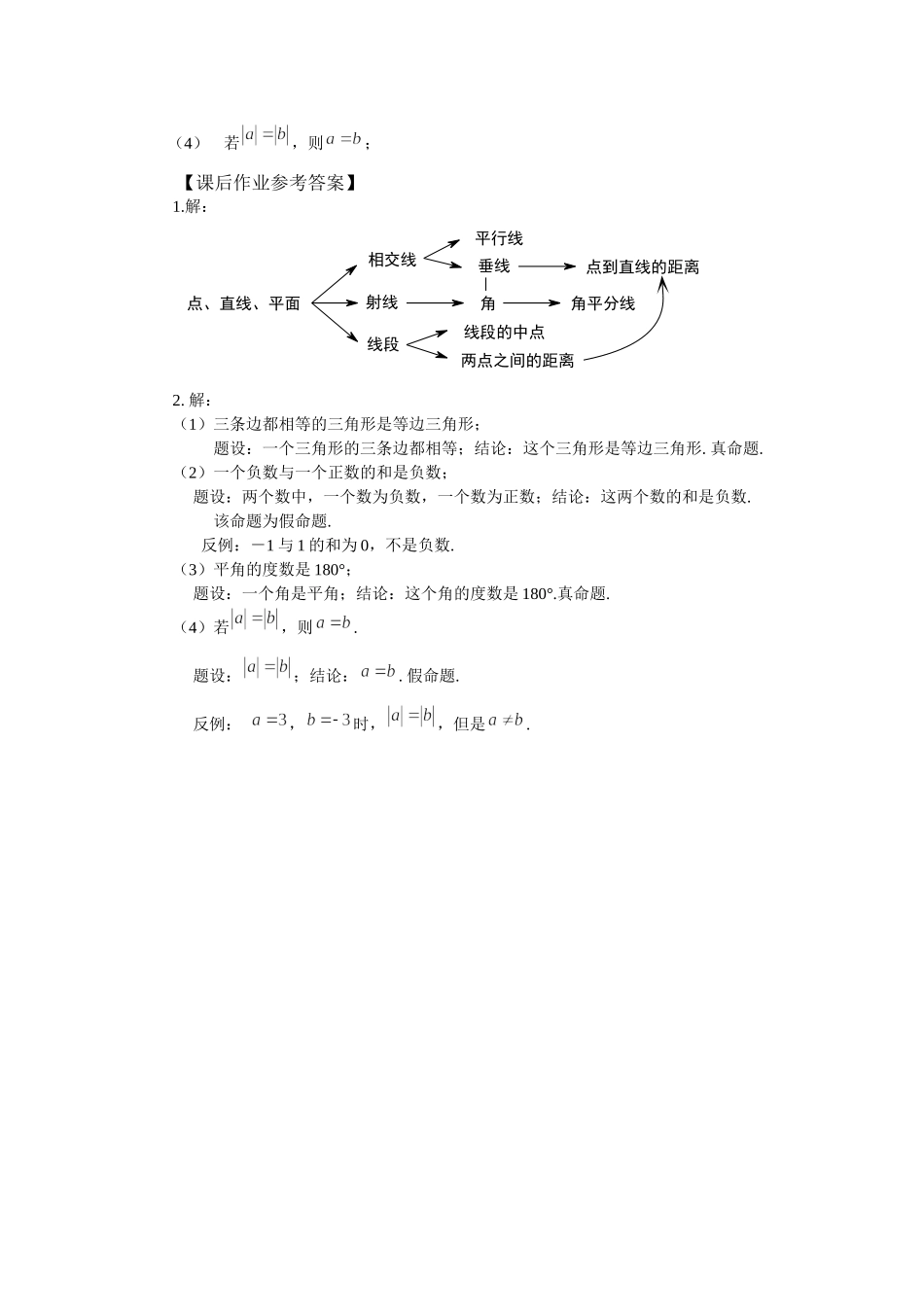
《简单的几何图形与推理》学习任务单【学习目标】1.了解概念、命题与推理的含义及其相关概念,会区分命题的题设与结论;2.了解概念体系,命题体系,初步感知公理体系和演绎推理的结构——三段论,感受概念——命题——推理——证明这一逻辑链,对几何的学习有一个比较完整的认识。发展抽象概括能力和推理能力。3.感悟学习的方法,进行知识的再认与构建。【课上任务】1.小学几何学习与初中几何学习的不同主要有哪些?2.什么叫定义?你能举出哪些定义的例子?3.概念与词或词组(名词或术语)的关系是什么?4.概念主要包括哪两个方面?5.给概念下定义有什么好处?6.给三角形进行分类的作用是什么?7.什么叫命题?8.一个命题包括哪两部分?9.什么是真命题?什么是假命题?10.如何判断一个命题是假命题?11.如何寻找一个命题的题设和结论?12.什么是初始概念、导出概念、基本事实和定理?13.通过今天的学习,你知道了哪些基本事实?14.什么是归纳推理?你能举出生活中或数学中的例子吗?15.什么是演绎推理?你能举出生活中或数学中的例子吗?16.什么是三段论?能否举出一个生活中或数学中的例子?17.证明一个命题的一般步骤有哪些?18.概念、命题、推理之间的关系是什么?例请判断下面的语句是不是命题?1.如果两条直线平行,那么这两条直线不相交.2.垂直于同一直线的两条直线平行吗?3.作一条线段等于已知线段.4.如果a=b,c=d,那么a+c=b+d.例找出命题的题设与结论,并判断命题的真假.1.如果两条直线平行,那么这两条直线不相交.2.如果a=b,c=d,那么a+c=b+d.3.等于同一个量的两个量相等.4.两个锐角的和一定是钝角练习:根据三段论推理形式填空.1.等量加等量和相等.因为a=b,c=d,所以.2.凡直角都相等.因为,所以∠1=∠2.3.等量的同倍量相等.因为a=b,c为常数,所以.4..因为三角形ABC是等腰三角,所以三角形ABC的两个底角相等.练习:找出下面三段论中的错误,并说明理由(1)水中的动物都是鱼——大前提因为鲸鱼在水中——小前提所以鲸鱼是鱼——结论(2)会飞的都是鸟——大前提因为麻雀会飞——小前提所以麻雀是鸟——结论(3)等量减等量差相等因为∠1=3∠,所以∠2=4.∠(4)同底数的幂相乘,底数不变,指数相加因为是同底数幂相乘的运算,所以(底数不变,指数相乘)【课后作业】1.请参考概念的学习,依据概念的发展,画出下列概念之间的关系示意图。“点、直线、平面、射线、线段、角、角平分线、平行线、相交线、垂线、线段的中点、两...