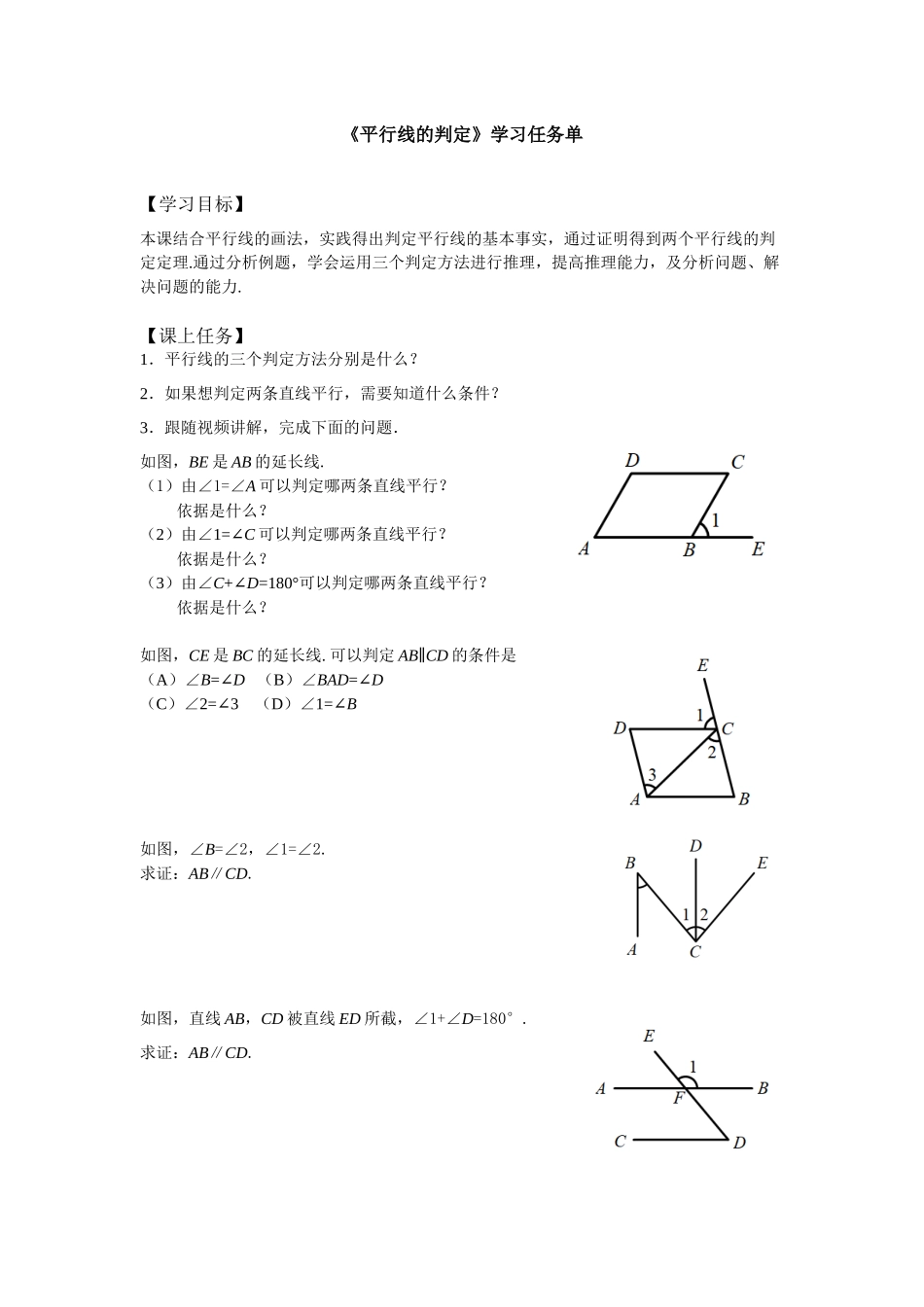
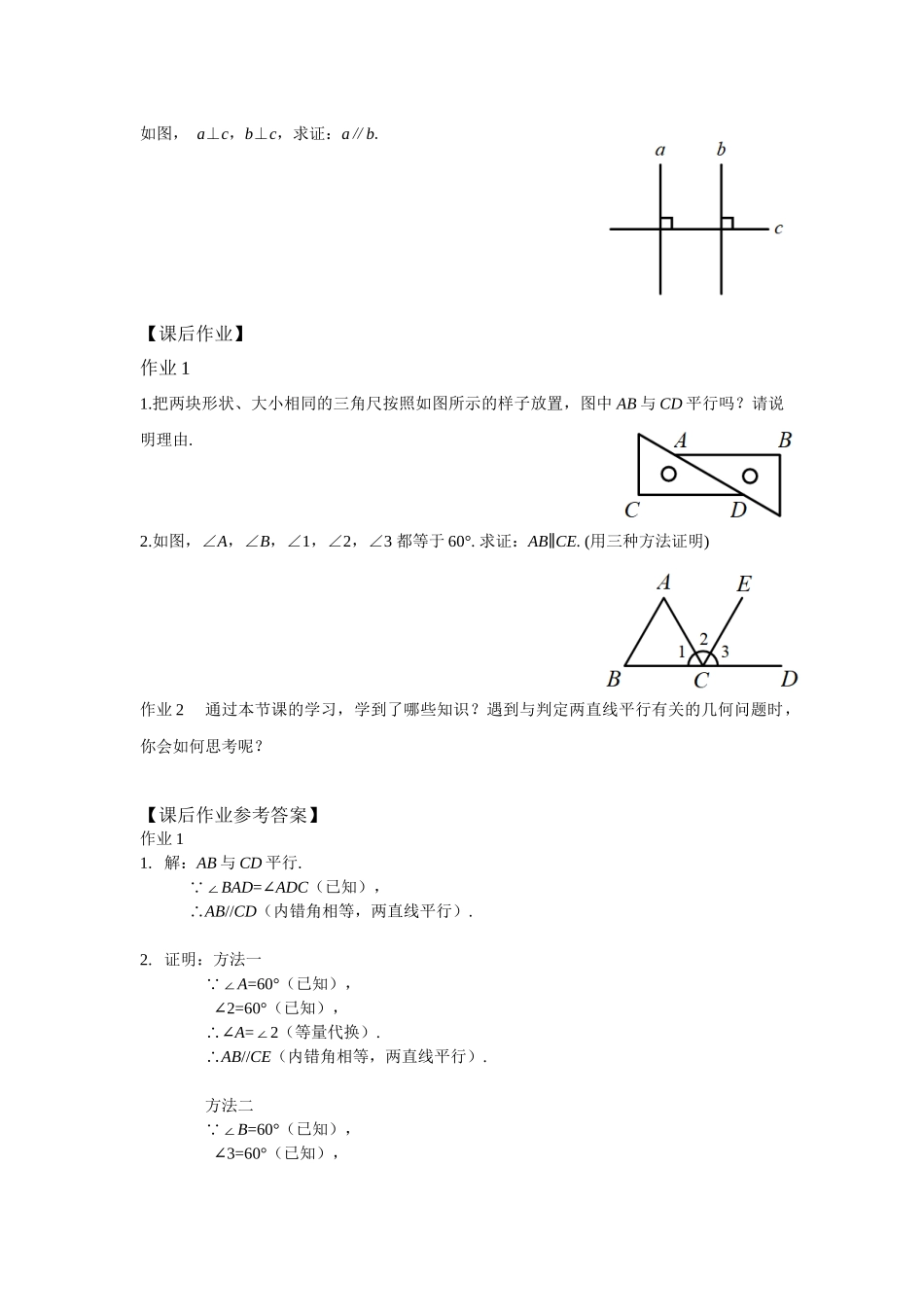
《平行线的判定》学习任务单【学习目标】本课结合平行线的画法,实践得出判定平行线的基本事实,通过证明得到两个平行线的判定定理.通过分析例题,学会运用三个判定方法进行推理,提高推理能力,及分析问题、解决问题的能力.【课上任务】1.平行线的三个判定方法分别是什么?2.如果想判定两条直线平行,需要知道什么条件?3.跟随视频讲解,完成下面的问题.如图,BE是AB的延长线.(1)由∠1=∠A可以判定哪两条直线平行?依据是什么?(2)由∠1=∠C可以判定哪两条直线平行?依据是什么?(3)由∠C+∠D=180°可以判定哪两条直线平行?依据是什么?如图,CE是BC的延长线.可以判定AB∥CD的条件是(A)∠B=∠D(B)∠BAD=∠D(C)∠2=3∠(D)∠1=∠B如图,∠B=∠2,∠1=∠2.求证:AB∥CD.如图,直线AB,CD被直线ED所截,∠1+∠D=180°.求证:AB∥CD.如图,a⊥c,b⊥c,求证:a∥b.【课后作业】作业11.把两块形状、大小相同的三角尺按照如图所示的样子放置,图中AB与CD平行吗?请说明理由.2.如图,∠A,∠B,∠1,∠2,∠3都等于60°.求证:AB∥CE.(用三种方法证明)作业2通过本节课的学习,学到了哪些知识?遇到与判定两直线平行有关的几何问题时,你会如何思考呢?【课后作业参考答案】作业11.解:AB与CD平行.∵∠BAD=∠ADC(已知),∴AB//CD(内错角相等,两直线平行).2.证明:方法一∵∠A=60°(已知),∠2=60°(已知),∴∠A=∠2(等量代换).∴AB//CE(内错角相等,两直线平行).方法二∵∠B=60°(已知),∠3=60°(已知),∴∠B=∠3(等量代换).∴AB//CE(同位角相等,两直线平行).方法三∵∠1=60°(已知),∠2=60°(已知),∴∠1+∠2=120°(等量加等量,和相等).即∠BCE=120°∵∠B=60°(已知),∴∠B+∠BCE=180°(等量加等量,和相等).∴AB//CE(同旁内角互补,两直线平行).作业2:略