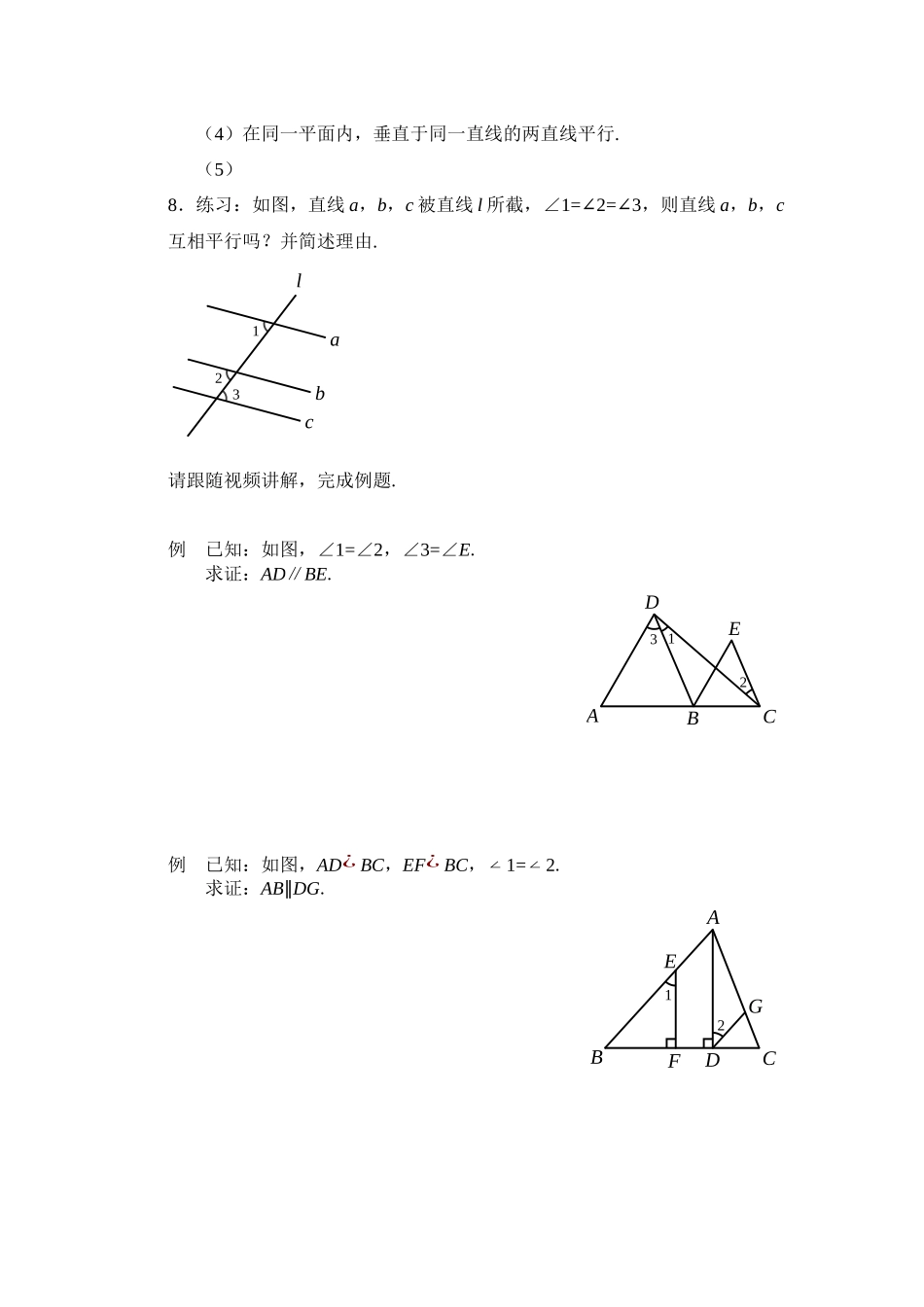
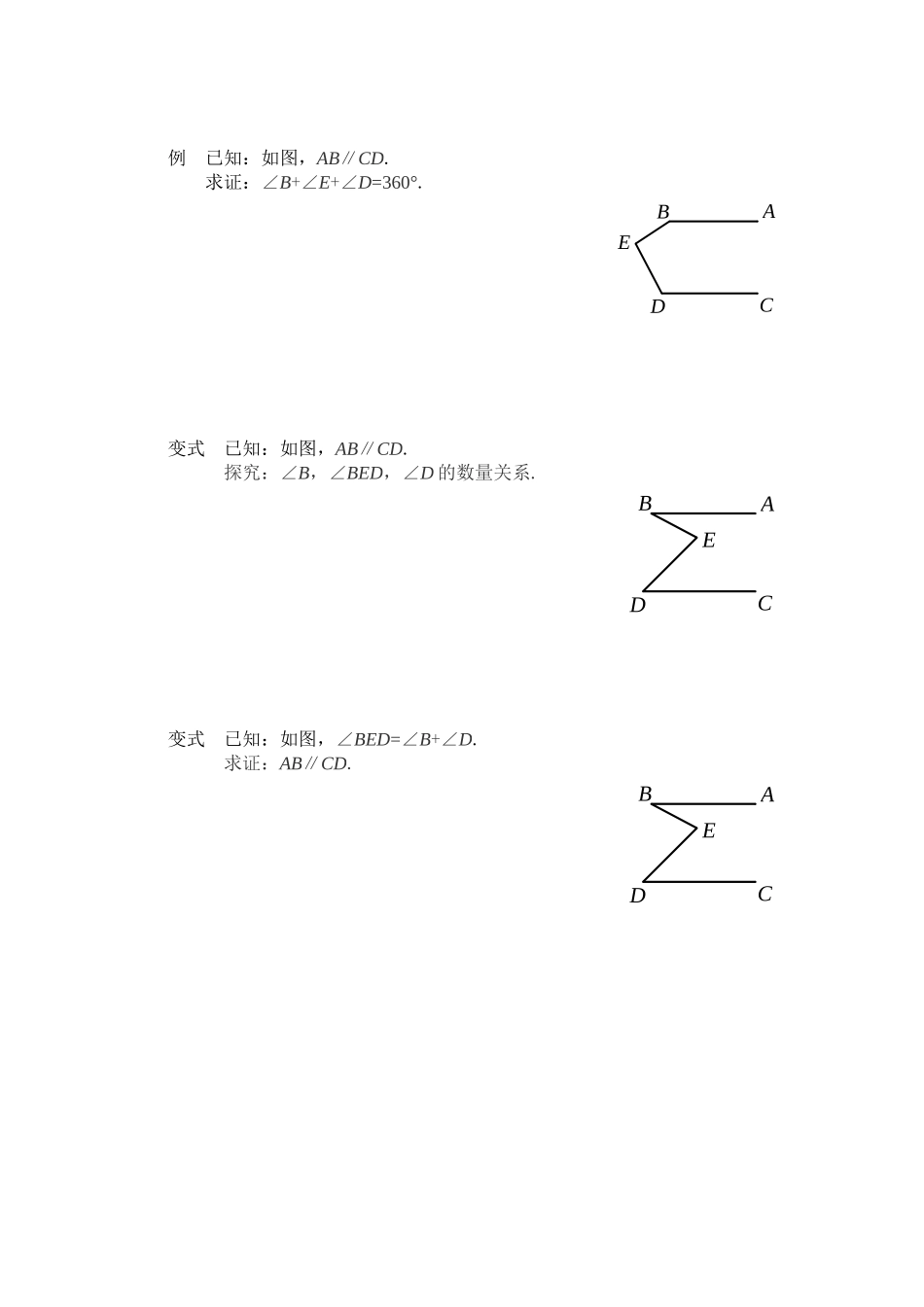
《平行线的性质和判定的综合运用》学习任务单【学习目标】本节课的主要内容是在辨析平行线的性质和判定的基础上,综合利用平行线的性质和判定及推论,运用综合法、分析法,经历证明、归纳等数学活动;发展学生的推理能力;共设计三道例题.课堂中将通过三道例题来帮助学生完成以上的学习任务.【课上任务】1.请同学们在笔记本上画图:过直线a外的点B和点C分别画直线a的平行线,能画出几条?aCB2.通过画图,我们知道b∥a,c∥a,你还能够从图中得到哪些结论呢?猜想:3.“平行于同一直线的两直线平行”这个命题的题设和结论分别是什么?4.把“平行于同一直线的两直线平行”改写成“如果……,那么……”的形式.5.根据命题的题设和结论,写出已知和求证.已知:求证:cba6.平行公理的推论是什么?7.小结平行线的判定方法.(1)同位角相等,两直线平行.(2)内错角相等,两直线平行.(3)同旁内角互补,两直线平行.(4)在同一平面内,垂直于同一直线的两直线平行.(5)8.练习:如图,直线a,b,c被直线l所截,∠1=2=3∠∠,则直线a,b,c互相平行吗?并简述理由.labc321请跟随视频讲解,完成例题.例已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.321EDACB例已知:如图,AD¿BC,EF¿BC,∠1=∠2.求证:AB∥DG.21GFDABCE例已知:如图,AB∥CD.求证:∠B+∠E+∠D=360°.CDEAB变式已知:如图,AB∥CD.探究:∠B,∠BED,∠D的数量关系.BAEDC变式已知:如图,∠BED=∠B+∠D.求证:AB∥CD.BAEDC变式已知:如图,当∠B,∠BED,∠D之间具有怎样的数量关系时,AB∥CD?CDEABBAEDC【课后作业】作业1:如图,已知AB∥CD,∠B=120°,∠C=25°,求∠BEC=.作业2:已知:如图,∠1+∠2=180°,∠3=∠B.求证:∠AED=∠C.321FEBCADG25°120°DEABC【课后作业参考答案】作业1参考答案:∠BEC=85°.作业2参考答案:解:∵∠1+4=180°∠(邻补角的定义)又∵∠1+2=180°∠(已知)∴∠2=4∠(同角的补角相等)∴AB∥EF(内错角相等,两直线平行)∴∠3=5∠(两直线平行,内错角相等)∵∠3=∠B(已知)∴5=∠∠B(等量代换)∴DE∥BC(同位角相等,两直线平行)∴∠AED=∠C(两直线平行,同位角相等)54321FEBCADG