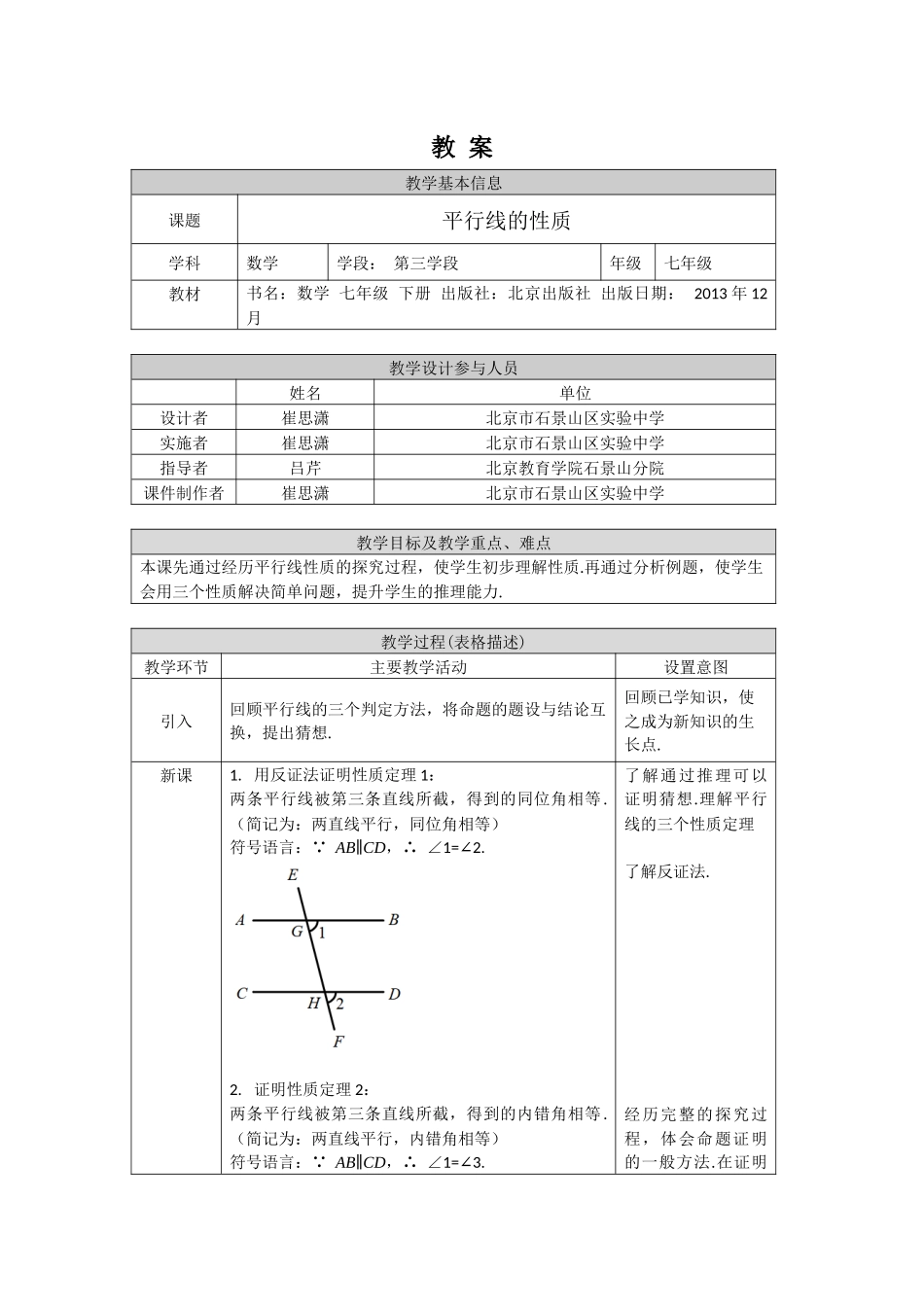
教案教学基本信息课题平行线的性质学科数学学段:第三学段年级七年级教材书名:数学七年级下册出版社:北京出版社出版日期:2013年12月教学设计参与人员姓名单位设计者崔思潇北京市石景山区实验中学实施者崔思潇北京市石景山区实验中学指导者吕芹北京教育学院石景山分院课件制作者崔思潇北京市石景山区实验中学教学目标及教学重点、难点本课先通过经历平行线性质的探究过程,使学生初步理解性质.再通过分析例题,使学生会用三个性质解决简单问题,提升学生的推理能力.教学过程(表格描述)教学环节主要教学活动设置意图引入回顾平行线的三个判定方法,将命题的题设与结论互换,提出猜想.回顾已学知识,使之成为新知识的生长点.新课1.用反证法证明性质定理1:两条平行线被第三条直线所截,得到的同位角相等.(简记为:两直线平行,同位角相等)符号语言: AB∥CD,∴∠1=2.∠2.证明性质定理2:两条平行线被第三条直线所截,得到的内错角相等.(简记为:两直线平行,内错角相等)符号语言: AB∥CD,∴∠1=3.∠了解通过推理可以证明猜想.理解平行线的三个性质定理了解反证法.经历完整的探究过程,体会命题证明的一般方法.在证明3.证明性质定理3:两条平行线被第三条直线所截,得到的同旁内角互补.(简记为:两直线平行,同旁内角互补)符号语言: AB∥CD,∴∠1+4=180°.∠定理的过程中,感受命题间的关系,发展推理能力.例题如图,平行线AB,CD被直线CE所截,∠C=50°.(1)∠1的度数为50°;(2)∠2的度数为130°;(3)∠3的度数为50°.如图,BE,DF分别是AB,CD的延长线.有以下五个与∠A有关的结论:①∠A=∠1;②∠A=∠2;③∠A=∠C;④∠A+∠3=180°;⑤∠A+∠4=180°.其中,能由AE∥CF得到的是②⑤;能由AD∥BC得到的是①④.如图,AD是BA的延长线,AE∥BC,∠1=∠2.求证:∠B=∠C.证明: AE∥BC(已知),∴∠1=∠B(两直线平行,同位角相等),∠2=∠C(两直线平行,内错角相等). ∠1=∠2(已知),∴∠B=∠C(等量代换).如图,AB∥DE,BC∥EF,求证:∠B=∠E.证明: AB∥DE(已知),∴∠B=∠1(两直线平行,同位角相等). BC∥EF(已知),∴∠E=∠1(两直线平行,同位角相等).∴∠B=∠E(等量代换).如图,∠A+∠D=180°,求证:∠B+∠C=180°.证明: ∠A+∠D=180°(已知),∴AD∥BC(同旁内角互补,两直线平行).通过例题讲解,使学生会用三个性质解决简单问题,提升学生的推理计算能力.本题着重使学生体会平行线的性质可以...