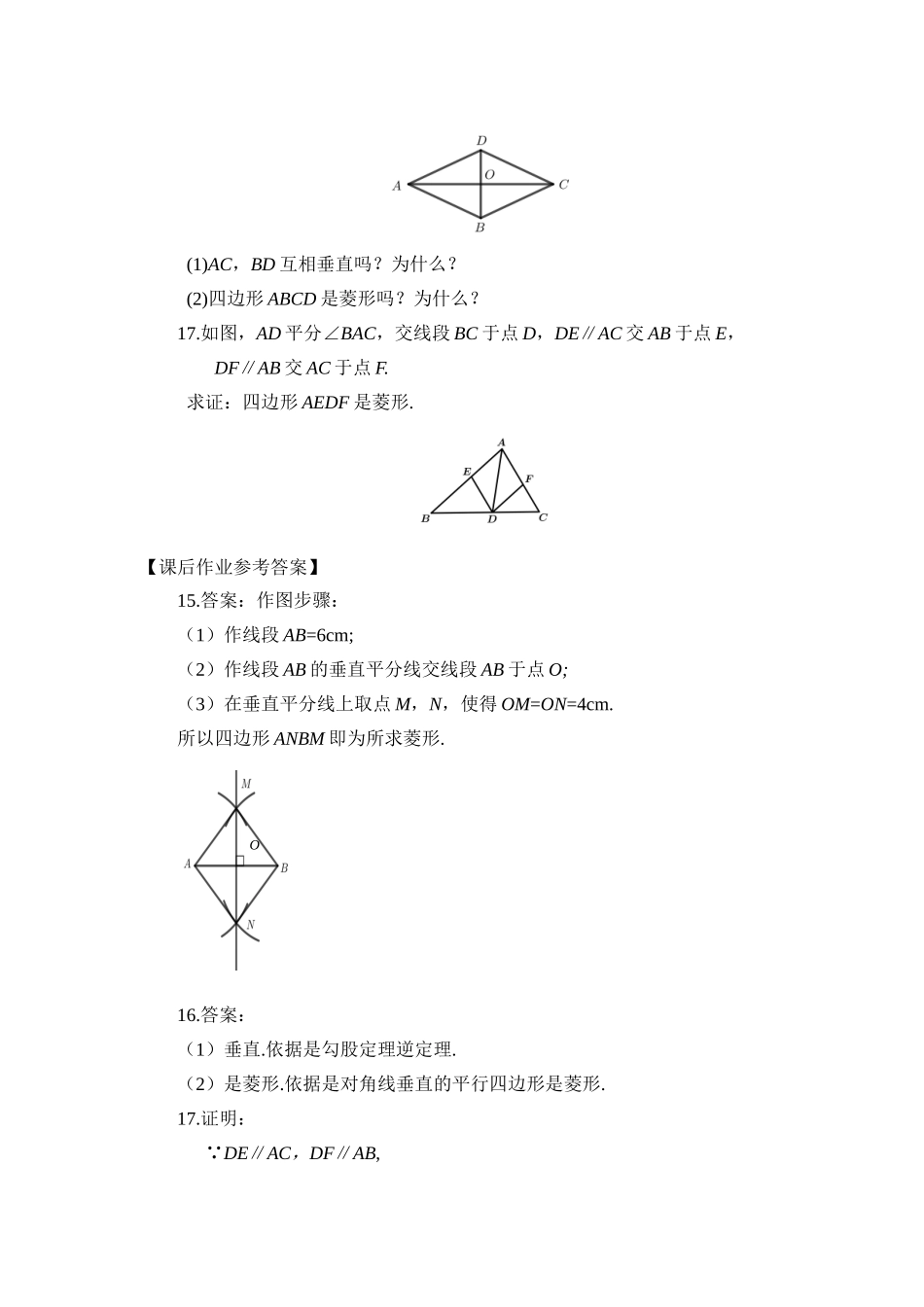
《菱形的判定》学习任务单【学习目标】掌握菱形的三种判定方法,能根据不同的已知条件,选择适当的判定定理进行推理和计算;经历菱形判定定理的探究过程,渗透类比思想,体会研究图形判定的一般思路;在探究和应用的过程中提高几何直观能力和推理能力.学习重点:菱形的判定及应用.学习难点:菱形的判定的探索及解题思路的体会.本节课共2道例题.【课上任务】1.如何检测所制作的窗格是否是菱形?需要测量哪些数据?2.矩形的定义、性质和判定内容是什么?它们之间有什么关系?矩形的三个判定定理是如何得到的?3.类比矩形判定的探究过程思考如何探究菱形的判定?4.对菱形的特殊性质进行题设和结论对调,你能得到哪些猜想呢?如何证明它们呢?5.菱形的判定方法有哪些?具体内容是什么?6.如何用尺规作图的方法得到菱形呢?7.题目中的解题思路是什么?你能归纳这些解题思路吗?【学习疑问】(可选)8.哪段证明过程理解有困难?9.性质和判定之间的关系不清楚?10.具体的解题思路比较不清晰?11.尺规作图没有掌握好?12.您想向同伴提出什么问题?13.您想向老师提出什么问题?14.没看懂的地方具体问题在哪?【课后作业】15.画一个菱形,使它的两条对角线长分别是6cm和8cm.16.如图,□ABCD的对角线AC与BD交于点O,AB=,AO=2,OB=1.(1)AC,BD互相垂直吗?为什么?(2)四边形ABCD是菱形吗?为什么?17.如图,AD平分∠BAC,交线段BC于点D,DE∥AC交AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.【课后作业参考答案】15.答案:作图步骤:(1)作线段AB=6cm;(2)作线段AB的垂直平分线交线段AB于点O;(3)在垂直平分线上取点M,N,使得OM=ON=4cm.所以四边形ANBM即为所求菱形.16.答案:(1)垂直.依据是勾股定理逆定理.(2)是菱形.依据是对角线垂直的平行四边形是菱形.17.证明:∵DE∥AC,DF∥AB,O∴四边形AEDF是平行四边形.∵AD平分∠BAC,∴∠BAD=∠CAD.∵DF∥AB,∴∠BAD=∠ADF.∴∠CAD=∠ADF.∴AF=DF.∴平行四边形AEDF是菱形.