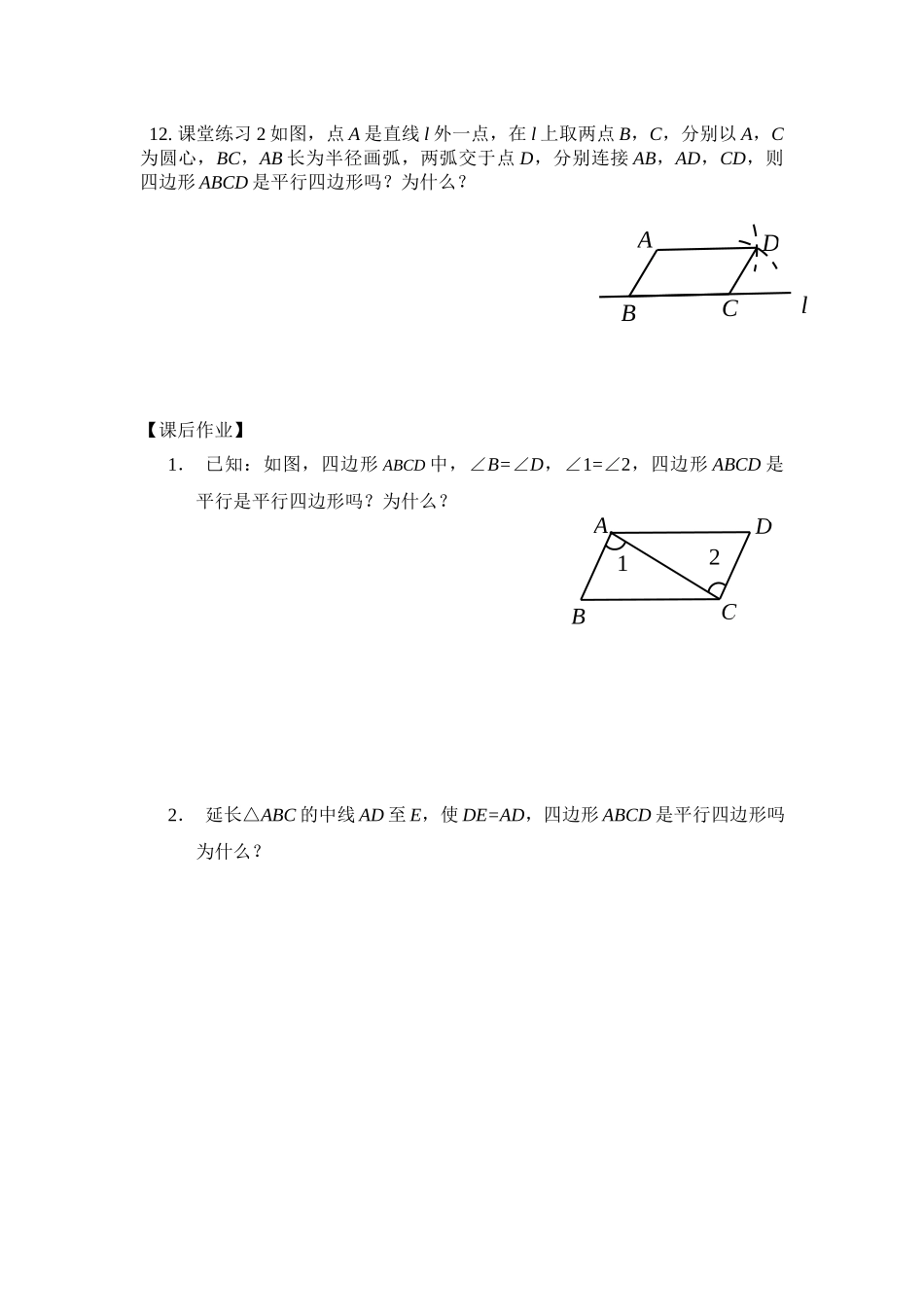
《平行四边形的判定第一课时》学习任务单【学习目标】1.了解平行四边形的判定方法的探索过程,体会类比,转化的思想及研究图形的一般思路.2.掌握平行四边形的判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.重点:平行四边形判定方法的探及应用.难点:平行四边形判定方法的理解和灵活应用.【课上任务】1.平行四边形的定义和性质的语言表述、图形、符号分别是什么?2.尝试写出平行四边形性质的逆命题?3.证明猜想1:两组对边分别平行的四边形是平行四边形.先画出图形,然后写出已知求证,并证明.4.写出平行四边形判定定理1的符号语言.5.证明猜想3:对角线互相平分的四边形是平行四边形,先画出图形,写出已知求证并证明.6.写出平行四边形判定定理2的符号语言.7.初识判定填空:(1))如图在四边形ABCD中,(1)若AB//CD,补充什么条件(),使四边形ABCD为平行四边形.(2)若AB=CD,补充条件(),使四边形ABCD为平行四边形.(3)若对角线AC,BD交于点O,OA=OC,OB=5,补充条件(),使四边形ABCD为平行四边形.DCBAABCDO3636ODCBA8.初识判定在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是()(A)AB∥CD,AD∥BC.(B)OA=OC,OB=OD.(C)AD=BC,AB∥CD.(D)AB=CD,AD=BC.9.例已知:如图,点E,F,G,H分别是□ABCD的边AB,BC,CD,DA上的点,且AE=CG,AH=CF.求证:四边形EFGH是平行四边形.10.例已知:如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别是OA,OC的中点.求证:四边形DEBF是平行四边形.11.课堂练习1.下列条件能判断四边形ABCD是平行四边形的().(A)AB∥CD,AC=BD.(B)AB=CD,AC=BD.(C)AB=CD,AD=BC.(D)AB=CD,OA=OC.ODCBAOFEDCBAODCBABHGFEDC12.课堂练习2如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD是平行四边形吗?为什么?【课后作业】1.已知:如图,四边形ABCD中,∠B=∠D,∠1=∠2,四边形ABCD是平行是平行四边形吗?为什么?2.延长△ABC的中线AD至E,使DE=AD,四边形ABCD是平行四边形吗为什么?21BDCAlDCBA【课后作业参考答案】1.是平行四边形.理由如下:在△ADC和△CBA中,∠B=∠D,∠1=∠2,AC=AC∴△ADC≌△CBA(AAS).∴AD=CB,CD=AB∴四边形ABCD是平行四边形.2.是平行四边形.理由如下:∵AD是△ABC的中线,∴BD=CD.∵DE=AD∴四边形ABEC是平行四边形.EDCBA