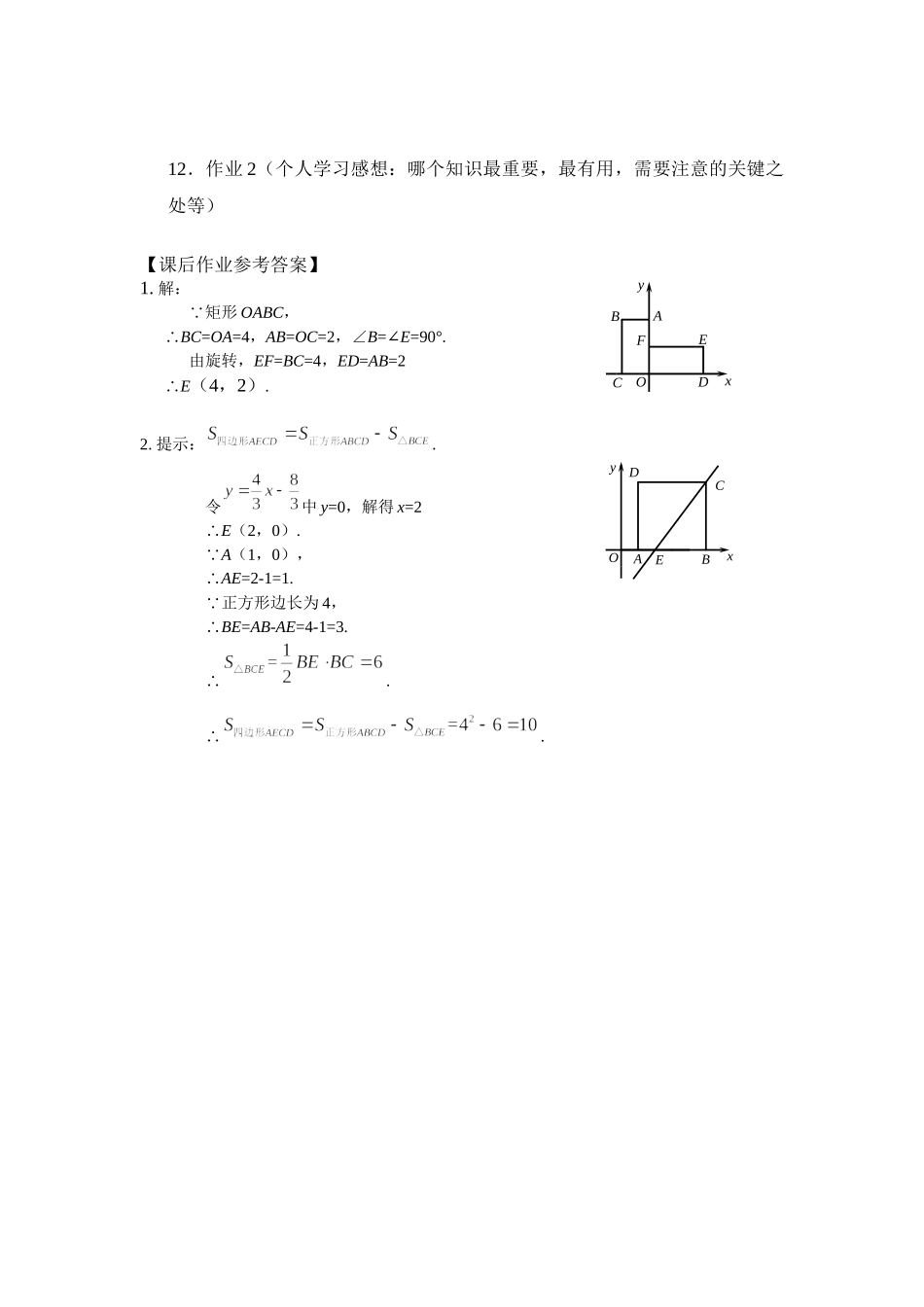
《坐标系中的特殊平行四边形》学习任务单【学习目标】本节课的主要内容是坐标系中的特殊平行四边形,需借助坐标系中特殊平行四边形顶点坐标间的特殊性,结合特殊平行四边形的性质解决问题,是对特殊平行四边形和坐标系相关知识的综合运用,利用代数方法解决几何问题,渗透数形结合思想.例题共3道.【课上任务】1.特殊平行四边形的性质有哪些?2.有一组对边与x轴平行的平行四边形的各个顶点坐标之间有什么联系?3.求特殊平行四边形顶点坐标问题的基本思路是什么?一般采用什么方法?4.处理坐标系中的特殊平行四边形问题时,需要注意什么??5.本节课涉及到的思想方法有哪些?【学习疑问】6.哪段文字没看明白?没看明白的文字,用自己的话怎么说?7.哪个环节没弄清楚?8.有什么困惑?9.您想向老师提出什么问题?10.本节课有几个环节,环节之间的联系和顺序?【课后作业】11.作业11.如图,把矩形OABC放在平面直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕原点顺时针旋转90°得到矩形ODEF,求点E的坐标.2.如图,平面直角坐标系中,正方形ABCD的边长为4,AB在x轴的正半轴上,点A的坐标是(1,0).经过点C的直线与x轴交于点E,求四边形AECD的面积.FEDBCAOxyEABDCOxy12.作业2(个人学习感想:哪个知识最重要,最有用,需要注意的关键之处等)【课后作业参考答案】1.解:∵矩形OABC,∴BC=OA=4,AB=OC=2,∠B=∠E=90°.由旋转,EF=BC=4,ED=AB=2∴E(4,2).2.提示:.令中y=0,解得x=2∴E(2,0).∵A(1,0),∴AE=2-1=1.∵正方形边长为4,∴BE=AB-AE=4-1=3.∴.∴.FEDBCAOxyEABDCOxy