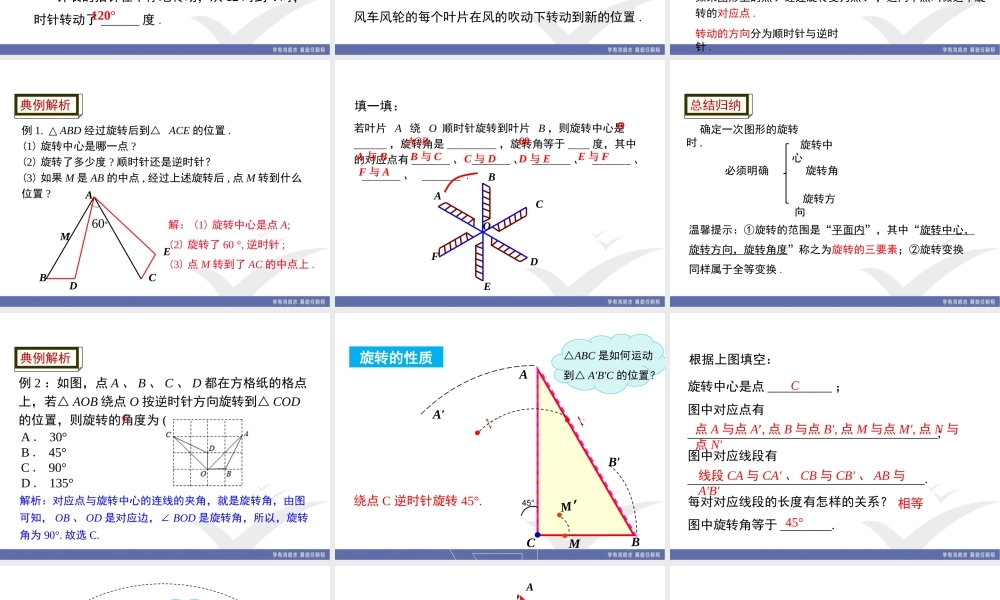
3.2图形的旋转第1课时旋转的概念和性质【学习目标】1.掌握旋转、旋转中心和旋转角的概念,并理解旋转的性质.2.能画出简单图形旋转后的对应图形.【学习重点】掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象.【学习难点】理解旋转的不变性,旋转角的性质,对应点到旋转中心的距离相等.教学目标这些运动有什么共同的特点?BOA450问题观察下列图形的运动,它有什么特点?旋转的概念钟表的指针在不停地转动,从12时到4时,时针转动了______度.120°把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.思考:怎样来定义这种图形变换?风车风轮的每个叶片在风的吹动下转动到新的位置.怎样来定义这种图形变换?把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.120OP′P旋转中心旋转角对应点旋转的定义这个定点称为旋转中心旋转中心.转动的角称为旋转角旋转角.转动的方向分为顺时针与逆时针.如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.知识要点例1.△ABD经过旋转后到△ACE的位置.(1)旋转中心是哪一点?(2)旋转了多少度?顺时针还是逆时针?(3)如果M是AB的中点,经过上述旋转后,点M转到什么位置?ABCEM.解:(1)旋转中心是点A;(2)旋转了60°,逆时针;(3)点M转到了AC的中点上.D60°典例解析若叶片A绕O顺时针旋转到叶片B,则旋转中心是______,旋转角是_________,旋转角等于____度,其中的对应点有_______、_______、_______、_______、_______、_______.OACDEFO∠AOB60F与AA与BB与CC与DD与EE与F填一填:B旋转中心旋转角旋转方向必须明确确定一次图形的旋转时,温馨提示:①旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度”称之为旋转的三要素;②旋转变换同样属于全等变换.总结归纳A.30°B.45°C.90°D.135°例2:如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为()解析:对应点与旋转中心的连线的夹角,就是旋转角,由图可知,OB、OD是对应边,∠BOD是旋转角,所以,旋转角为90°.故选C.C典例解析ABB′A′C.M′M....45°绕点C逆时针旋转45°.△ABC是如何运动到△A′B′C的位置?旋转的性质旋转中心是点__________;图中对应点有_______________________________________;图中对应线段有_____________________________________.每对对应...