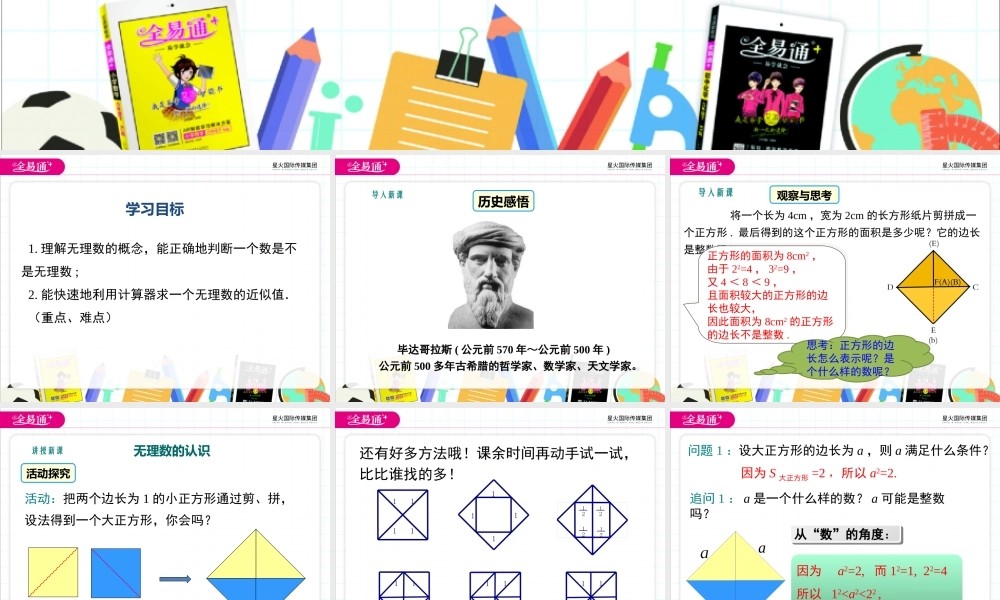
第3章实数3.1平方根第2课时1.理解无理数的概念,能正确地判断一个数是不是无理数;2.能快速地利用计算器求一个无理数的近似值.(重点、难点)学习目标导入新课历史感悟毕达哥拉斯(公元前570年~公元前500年)公元前500多年古希腊的哲学家、数学家、天文学家。导入新课将一个长为4cm,宽为2cm的长方形纸片剪拼成一个正方形.最后得到的这个正方形的面积是多少呢?它的边长是整数吗?正方形的面积为8cm2,由于22=4,32=9,又4<8<9,且面积较大的正方形的边长也较大,因此面积为8cm2的正方形的边长不是整数.正方形的面积为8cm2,由于22=4,32=9,又4<8<9,且面积较大的正方形的边长也较大,因此面积为8cm2的正方形的边长不是整数.观察与思考思考:正方形的边长怎么表示呢?是个什么样的数呢?活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?111讲授新课活动探究无理数的认识1212121211111111111111111111还有好多方法哦!课余时间再动手试一试,比比谁找的多!问题1:设大正方形的边长为a,则a满足什么条件?追问1:a是一个什么样的数?a可能是整数吗?aaa因为S大正方形=2,所以a2=2.从“数”的角度:从“数”的角度:因为a2=2,而12=1,22=4所以12