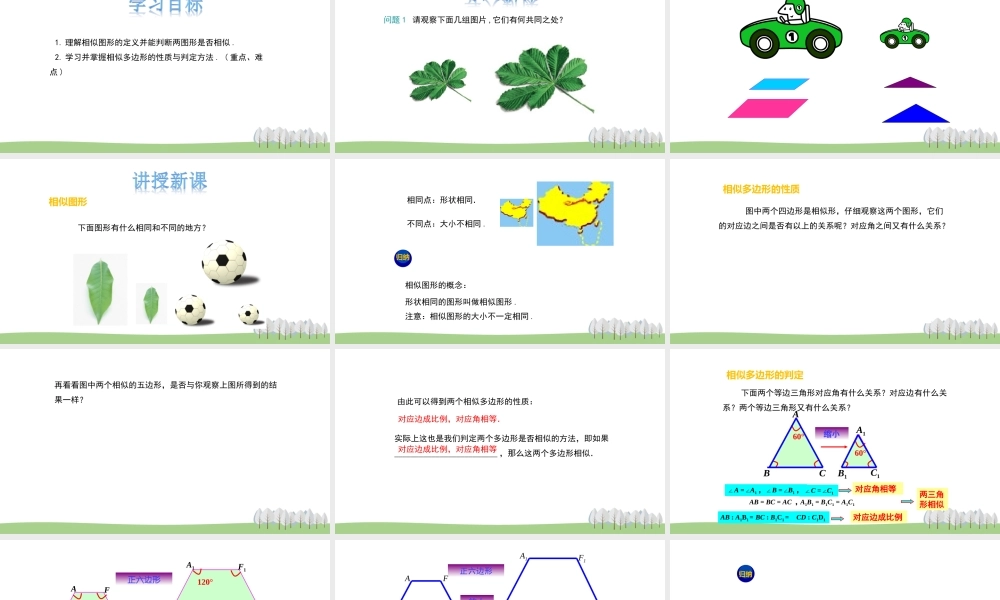
25.7相似多边形和图形的位似导入新课讲授新课当堂练习课堂小结第1课时相似多边形1.理解相似图形的定义并能判断两图形是否相似.2.学习并掌握相似多边形的性质与判定方法.(重点、难点)问题1请观察下面几组图片,它们有何共同之处?相似图形下面图形有什么相同和不同的地方?相同点:形状相同.不同点:大小不相同.相似图形的概念:形状相同的图形叫做相似图形.注意:相似图形的大小不一定相同.归纳相似多边形的性质图中两个四边形是相似形,仔细观察这两个图形,它们的对应边之间是否有以上的关系呢?对应角之间又有什么关系?再看看图中两个相似的五边形,是否与你观察上图所得到的结果一样?由此可以得到两个相似多边形的性质:实际上这也是我们判定两个多边形是否相似的方法,即如果_________________________,那么这两个多边形相似.对应边成比例,对应角相等对应边成比例,对应角相等.相似多边形的判定ABCA1B1C1缩小下面两个等边三角形对应角有什么关系?对应边有什么关系?两个等边三角形又有什么关系?∠A=∠A1,∠B=∠B1,∠C=∠C1AB:A1B1=BC:B1C1=CD:C1D1AB=BC=AC,A1B1=B1C1=A1C160°60°对应角相等对应边成比例两三角形相似放大120°120°∠A=∠A1,∠B=∠B1,∠C=∠C1对应角相等ABCA1B1C1FEDF1E1D1∠D=∠D1,∠E=∠E1,∠F=∠F1正六边形正六边形放大ABCA1B1C1FEDF1E1D1AB=BC=CD=DE=EF=FA,A1B1=B1C1=C1D1=D1E1=E1F1=F1A1对应边成比例AB:A1B1=BC:B1C1=CD:C1D1=DE:D1E1=EF:E1F1=FA:F1A1相似比:相似多边形对应边的比(相似比大于零).相似多边形的定义:两个边数相同的多边形,如果各边对应成比例,各角对应相等相等,就称这两个多边形相似,就称这两个多边形相似..归纳1.根据下图所示,这两个多边形相似吗?说说你的理由.140120759060806550不相似,对应边不成比例.2.如图,正方形的边长a=10,菱形的边长b=5,它们相似吗?请说明理由.不相似,对应边成比例,但对应角不相等.3.如图所示的两个矩形是否相似?不相似,大矩形的对应边成比例为20:1=5:3,但小矩形的对应边成比例为(20-6):(12-6)=12:6=7:3.3.相似比:相似多边形对应边的比(相似比大于零).1.相似多边形的性质:对应角相等对应角相等,对应边成比例,对应边成比例(对应边的比相等)..2.相似多边形的定义:两个边数相同的多边形,如果各边对应成比例,各角对应相等相等,就称这两个多边形相似,就称这两个多边形相似..