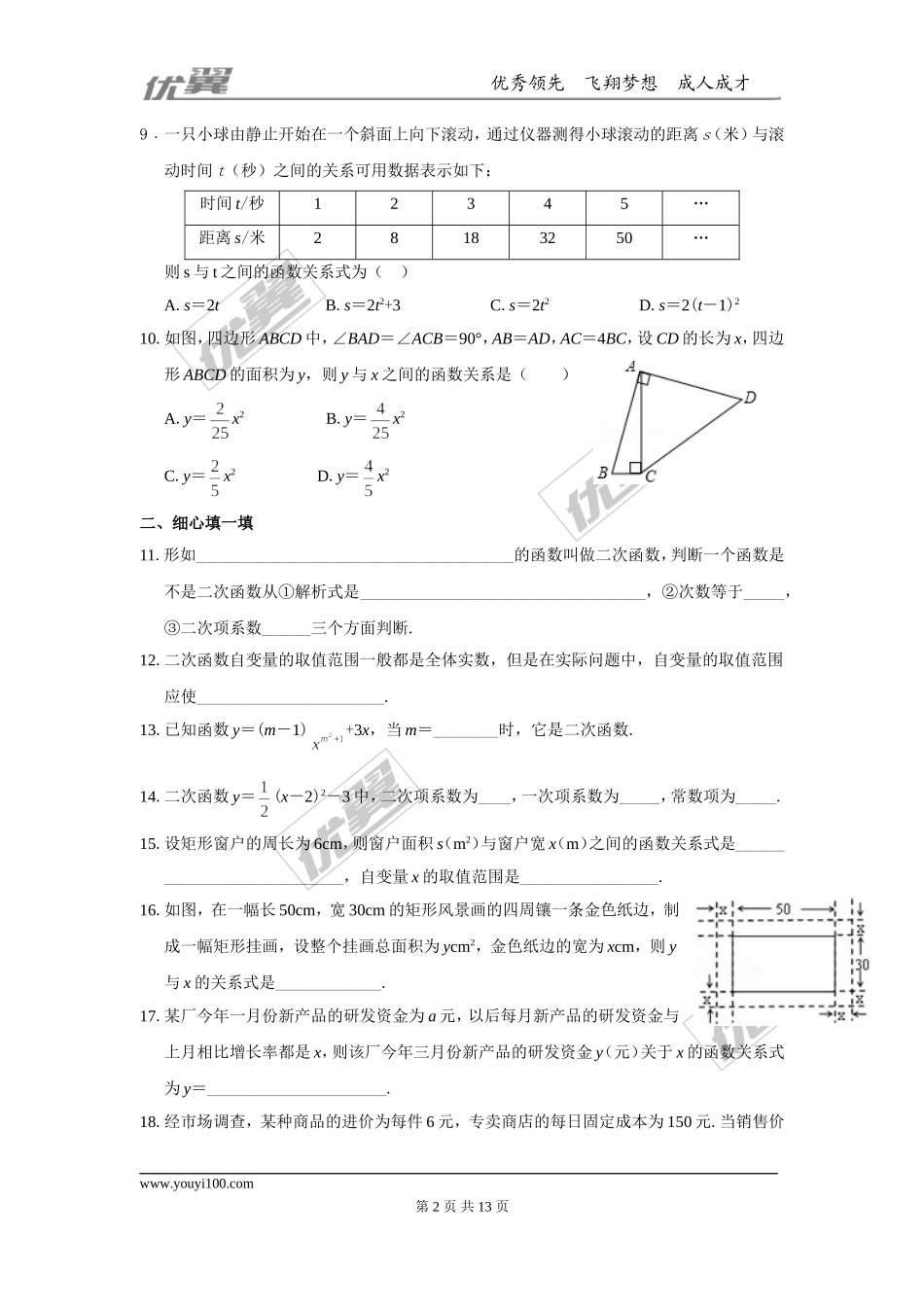
优秀领先飞翔梦想成人成才第21章二次函数与反比例函数周周测221.1一、精心选一选1﹒下列函数表达式中,一定为二次函数的是()A.y=3x-1B.y=ax2+bx+cC.s=2t2-2t+1D.y=x2+2﹒已知函数y=(m2+m)x2+mx+4为二次函数,则m的取值范围是()A.m≠0B.m≠-1C.m≠0,且m≠-1D.m=-13﹒已知二次函数y=1-3x+x2,则其二次项系数a,一次项系数b,常数项c分别是()A.a=1,b=-3,c=B.a=1,b=3,c=C.a=,b=3,c=1D.a=,b=-3,c=14﹒若二次函数y=4x2+1的函数值为5,则自变量x的值应为()A.1B.-1C.±1D.5﹒已知二次函数y=3(x-2)2+1,当x=3时,y的值为()A.4B.-4C.3D.-36﹒下列函数关系中,满足二次函数关系的是()A.距离一定时,汽车行驶的速度与时间之间的关系B.等边三角形的周长与边长之间的关系C.在弹性限度内,弹簧的长度与所挂物体的质量之间的关系D.圆的面积与半径之间的关系7﹒矩形的周长为24cm,其中一边为xcm(其中x>0),面积为ycm2,则这样的矩形中y与x的关系可以写成()A.y=x2B.y=12-x2C.y=(12-x)xD.y=2(12-x)8﹒某工厂一种产品的年产量是20件,如果每一年都比上一年的产品增加x倍,两年后产品产量y与x的函数关系是()A.y=20(1-x)2B.y=20+2xC.y=20(1+x)2D.y=20+20x+20x2www.youyi100.com第1页共13页优秀领先飞翔梦想成人成才9﹒一只小球由静止开始在一个斜面上向下滚动,通过仪器测得小球滚动的距离s(米)与滚动时间t(秒)之间的关系可用数据表示如下:时间t/秒12345…距离s/米28183250…则s与t之间的函数关系式为()A.s=2tB.s=2t2+3C.s=2t2D.s=2(t-1)210.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系是()A.y=x2B.y=x2C.y=x2D.y=x2二、细心填一填11.形如_______________________________________的函数叫做二次函数,判断一个函数是不是二次函数从①解析式是___________________________________,②次数等于_____,③二次项系数______三个方面判断.12.二次函数自变量的取值范围一般都是全体实数,但是在实际问题中,自变量的取值范围应使_______________________.13.已知函数y=(m-1)+3x,当m=________时,它是二次函数.14.二次函数y=(x-2)2-3中,二次项系数为____,一次项系数为_____,常数项为_____.15.设矩形窗户的周长为6cm,则窗户面积s(m2)与窗户宽x(m)之间的函数关系式是______________________...