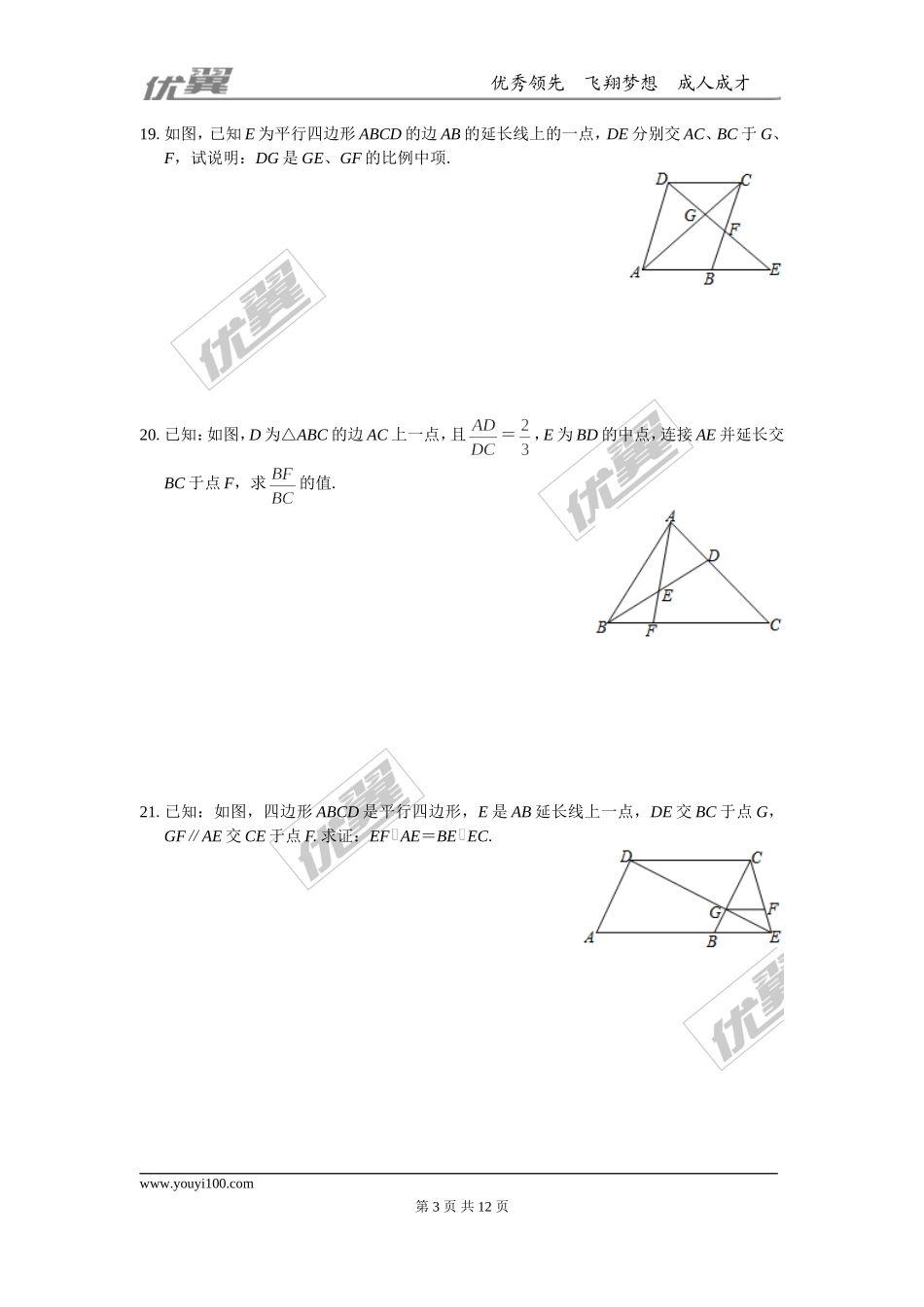
优秀领先飞翔梦想成人成才第22章相似形周周测122.1比例线段一、精心选一选1﹒若=,则的值为()A.1B.C.D.2﹒下列判断正确的是()A.所有的等腰三角形都相似B.所有的等腰直角三角形都相似C.所有的矩形都相似D.所有的菱形都相似3﹒在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是()A.1250kmB.125kmC.12.5kmD.1.25km4﹒如果a=3,b=2,且b是a和c的比例中项,那么c等于()A.±B.C.D.±5﹒下列长度的各组线段中,能组成比例线段的是()A.2,5,6,8B.3,6,9,18C.1,2,3,4D.3,6,7,96﹒如图,已知点C是线段AB的黄金分割点(其中AC>BC),则下列结论中正确的是()A.AB2=AC2+BC2B.BC2=ACBAC.=D.=7﹒如图,直线l1∥l2∥l3,直线AC分别交11,l2,l3于点A、B、C,直线DF分别交11,l2,l3于点D、E、F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为()A.B.2C.D.第7题图第8题图第9题图第10题图8﹒如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为()A.1B.2C.3D.49﹒如图,AB与CD相交于点O,AB∥CD,若AO=2,DO=3,BC=6,则CO等于()A.2.4B.3C.3.6D.410.如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是()A.=B.=C.=D.=www.youyi100.com第1页共12页优秀领先飞翔梦想成人成才二、细心填一填11.已知==≠0,则的值为_________.12.已知=,则=________.13.已知实数x、y、z满足x+y+z=0,3x-y-2z=0,则x:y:z=_______.14.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,AD=2,BC=5,则EC=________.15.如图,点D是△ABC边BC上的中点,点E在边AC上,且=,AD与BE相交于点O,则=_________.第14题图第15题图第16题图16.如图,已知△ABC中,D为BC中点,E,F为AB边三等分点,AD分别交CE,CF于点M,N,则AM:MN:ND等于______________.三、解答题17.已知a,b,c为△ABC的三边长,且a+b+c=36,==,求△ABC的三边长.18.如图,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且=.求证:AD=EB.www.youyi100.com第2页共12页优秀领先飞翔梦想成人成才19.如图,已知E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.20.已知:如图,D为△ABC的边AC上一点,且=,E为BD的中点,连接AE并延长交BC于点F,求的值.21.已知:如图,四边形ABCD是平行四边形,E是AB延长线上一点,DE交BC于点G,GF∥AE交CE于点F.求证...