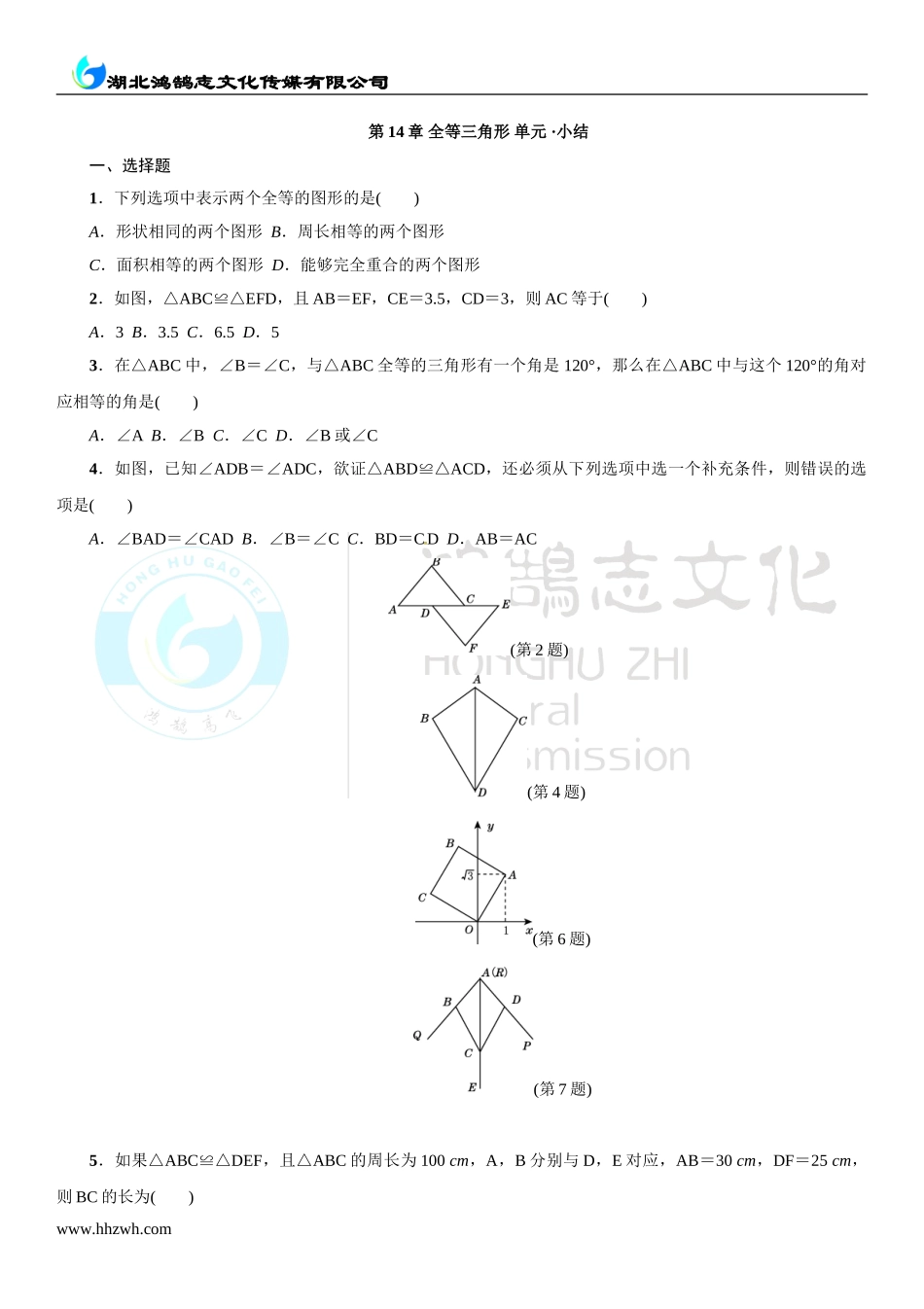
湖北鸿鹄志文化传媒有限公司第14章全等三角形单元·小结一、选择题1.下列选项中表示两个全等的图形的是()A.形状相同的两个图形B.周长相等的两个图形C.面积相等的两个图形D.能够完全重合的两个图形2.如图,△ABC≌△EFD,且AB=EF,CE=3.5,CD=3,则AC等于()A.3B.3.5C.6.5D.53.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是120°,那么在△ABC中与这个120°的角对应相等的角是()A.∠AB.∠BC.∠CD.∠B或∠C4.如图,已知∠ADB=∠ADC,欲证△ABD≌△ACD,还必须从下列选项中选一个补充条件,则错误的选项是()A.∠BAD=∠CADB.∠B=∠CC.BD=CDD.AB=AC(第2题)(第4题)(第6题)(第7题)5.如果△ABC≌△DEF,且△ABC的周长为100cm,A,B分别与D,E对应,AB=30cm,DF=25cm,则BC的长为()www.hhzwh.com湖北鸿鹄志文化传媒有限公司A.45cmB.55cmC.30cmD.25cm6.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,),则点C的坐标为()A.(-,1)B.(-1,)C.(,1)D.(-,-1)7.(2015·绍兴)如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是()A.SASB.ASAC.AASD.SSS8.如图,∠1=∠2,AE⊥OB于E,BD⊥OA于D,AE与BD的交点为C,则图中全等三角形共有()A.2对B.3对C.4对D.5对9.如图,是一个4×4的正方形网格,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于()A.585°B.540°C.270°D.315°(第8题)(第9题)(第10题)10.如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是()①△BCD为等腰三角形;②BF=AC;③CE=BF;④BH=CE.A.①②B.①③C.①②③D.①②③④二、填空题11.如图,线段AD与BC相交于点O,连接AB、CD,且∠B=∠D,要使△AOB≌△COD,应添加一个条件是__________(只填一个即可).www.hhzwh.com湖北鸿鹄志文化传媒有限公司12.如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=________时,△ABC和△APQ全等.(第11题)(第12题)(第13题)(第14题)13.如图,在△ABC中,D、E分别是边AB、AC上的点,且DE...