北京课改初中数学八下《15.7一次函数的应用》PPT课件 (2).pptVIP免费

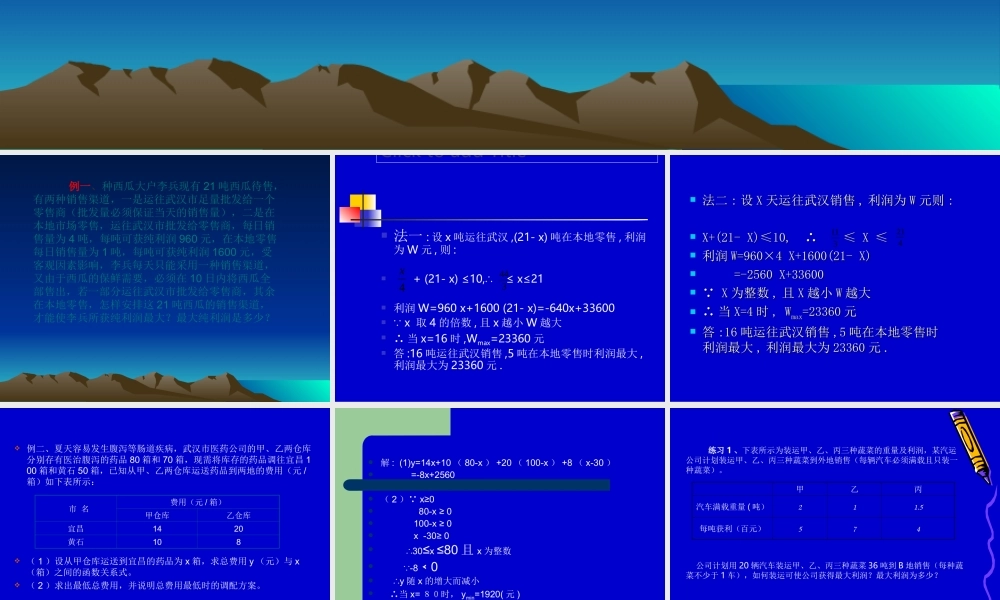
15.715.7一次函数的应用一次函数的应用例一、种西瓜大户李兵现有21吨西瓜待售，有两种销售渠道，一是运往武汉市足量批发给一个零售商（批发量必须保证当天的销售量），二是在本地市场零售，运往武汉市批发给零售商，每日销售量为4吨，每吨可获纯利润960元，在本地零售每日销售量为1吨，每吨可获纯利润1600元，受客观因素影响，李兵每天只能采用一种销售渠道，又由于西瓜的保鲜需要，必须在10日内将西瓜全部售出，若一部分运往武汉市批发给零售商，其余在本地零售，怎样安排这21吨西瓜的销售渠道，才能使李兵所获纯利润最大？最大纯利润是多少？ClicktoaddTitle法一:设x吨运往武汉,(21-x)吨在本地零售,利润为W元,则:+(21-x)≤10,∴≤x≤21利润W=960x+1600(21-x)=-640x+33600 x取4的倍数,且x越小W越大∴当x=16时,Wmax=23360元答:16吨运往武汉销售,5吨在本地零售时利润最大,利润最大为23360元.4x344法二法二::设设XX天运往武汉销售天运往武汉销售,,利润为利润为WW元则元则::X+(21-X)≤10,∴≤X≤X+(21-X)≤10,∴≤X≤利润利润W=960×4X+1600(21-X)W=960×4X+1600(21-X)=-2560X+33600=-2560X+33600 XX为整数为整数,,且且XX越小越小WW越大越大∴∴当当X=4X=4时时,W,Wmaxmax=23360=23360元元答答:16:16吨运往武汉销售吨运往武汉销售,5,5吨在本地零售时吨在本地零售时利润最大利润最大,,利润最大为利润最大为2336023360元元..311421例二、夏天容易发生腹泻等肠道疾病，武汉市医药公司的甲、乙两仓库分别存有医治腹泻的药品80箱和70箱，现需将库存的药品调往宜昌100箱和黄石50箱，已知从甲、乙两仓库运送药品到两地的费用（元/箱）如下表所示：（1）设从甲仓库运送到宜昌的药品为x箱，求总费用y（元）与x（箱）之间的函数关系式。（2）求出最低总费用，并说明总费用最低时的调配方案。市名费用（元/箱）甲仓库乙仓库宜昌1420黄石108解:(1)y=14x+10（80-x）+20（100-x）+8（x-30）=-8x+2560（2） x≥080-x≥0100-x≥0x-30≥0∴30≤x≤80且x为整数 -80﹤∴y随x的增大而减小∴当x=８０时，ymin=1920(元)答：甲运送３０箱到宜昌，５０箱到黄石；乙运送７０箱到宜昌，０箱到黄石时运费最低为１９２０元．练习1、下表所示为装运甲、乙、丙三种蔬菜的重量及利润，某汽运公司计划装运甲、乙、丙三种蔬菜到外地销售（每辆汽车必须满载且只装一种蔬菜）。公司计划用20辆汽车装运甲、乙、丙三种蔬菜36...