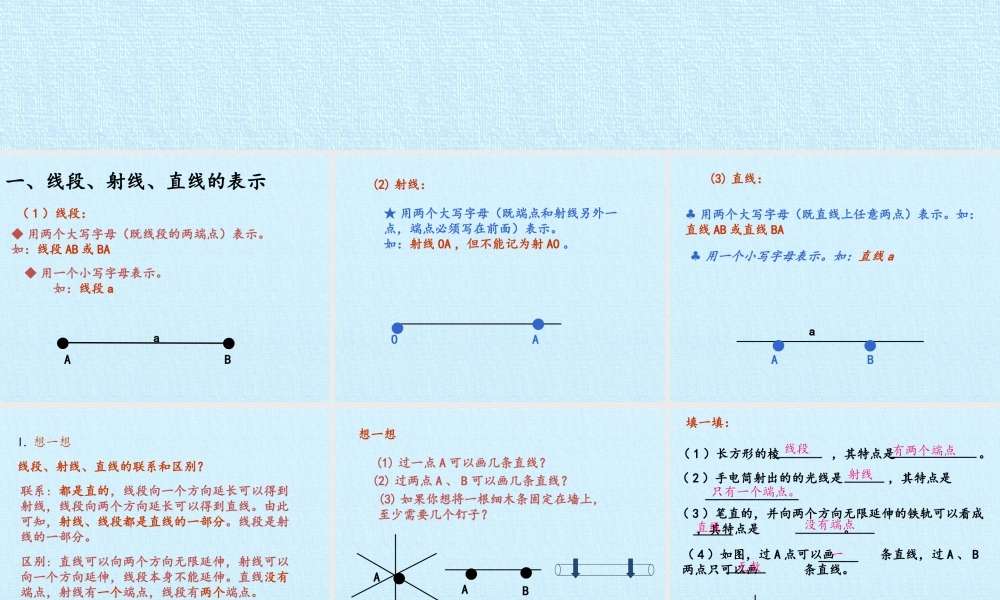
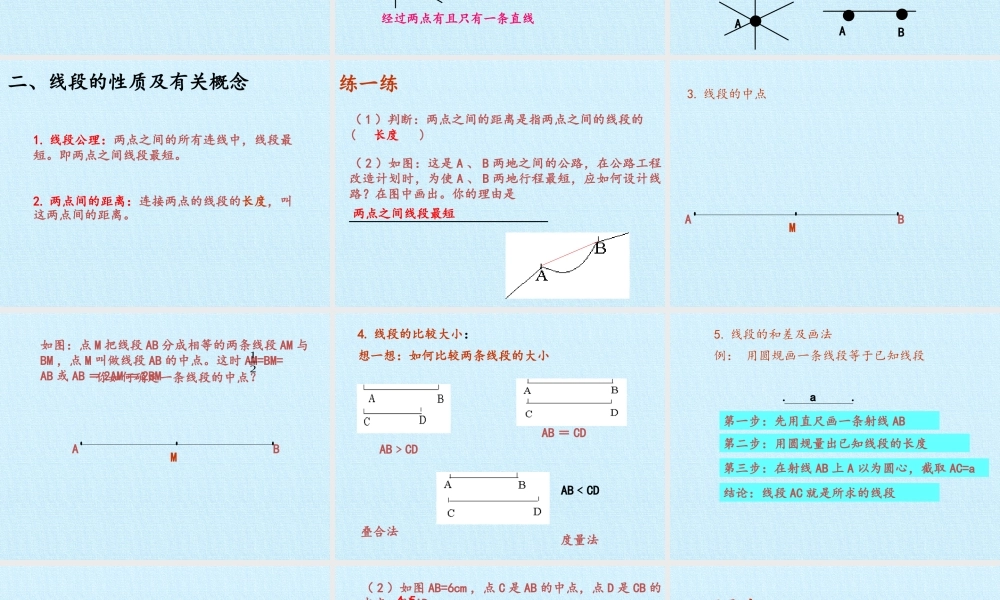
第七章线段与角的画法复习课件◆用一个小写字母表示。如:线段aa◆用两个大写字母(既线段的两端点)表示。如:线段AB或BA●●AB(1)线段:一、线段、射线、直线的表示★用两个大写字母(既端点和射线另外一点,端点必须写在前面)表示。如:射线OA,但不能记为射AO。●●OA(2)射线:♣用一个小写字母表示。如:直线aa♣用两个大写字母(既直线上任意两点)表示。如:直线AB或直线BA●●AB(3)直线:l.想一想线段、射线、直线的联系和区别?联系:都是直的,线段向一个方向延长可以得到射线,线段向两个方向延长可以得到直线。由此可知,射线、线段都是直线的一部分。线段是射线的一部分。区别:直线可以向两个方向无限延伸,射线可以向一个方向延伸,线段本身不能延伸。直线没有端点,射线有一个端点,线段有两个端点。想一想(1)过一点A可以画几条直线?●A(2)过两点A、B可以画几条直线?●●AB(3)如果你想将一根细木条固定在墙上,至少需要几个钉子?经过两点有且只有一条直线(2)手电筒射出的的光线是,其特点是填一填:(1)长方形的棱,其特点是。(3)笔直的,并向两个方向无限延伸的铁轨可以看成,其特点是。(4)如图,过A点可以画条直线,过A、B两点只可以画条直线。●A●●AB线段有两个端点射线只有一个端点。直线没有端点无数一1.线段公理:两点之间的所有连线中,线段最短。即两点之间线段最短。2.两点间的距离:连接两点的线段的长度,叫这两点间的距离。二、线段的性质及有关概念(2)如图:这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出。你的理由是_______________________________练一练长度两点之间线段最短(1)判断:两点之间的距离是指两点之间的线段的()3.线段的中点ABM你如何确定一条线段的中点?如图:点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点。这时AM=BM=AB或AB=2AM=2BM21ABM4.线段的比较大小:想一想:如何比较两条线段的大小叠合法度量法AB﹥CDAB=CDAB﹤CD例:用圆规画一条线段等于已知线段..a第一步:先用直尺画一条射线AB第二步:用圆规量出已知线段的长度第三步:在射线AB上A以为圆心,截取AC=a结论:线段AC就是所求的线段5.线段的和差及画法(1)如图,AD=AB-____=AC+_____BDCD试一试(2)如图AB=6cm,点C是AB的中点,点D是CB的中点,则AD=____cm(3)如图,下列说法,不能判断点C是线段AB的中点的是()A.AC=CBB.AB=2ACC.AC+CB=ABD.CB=AB...