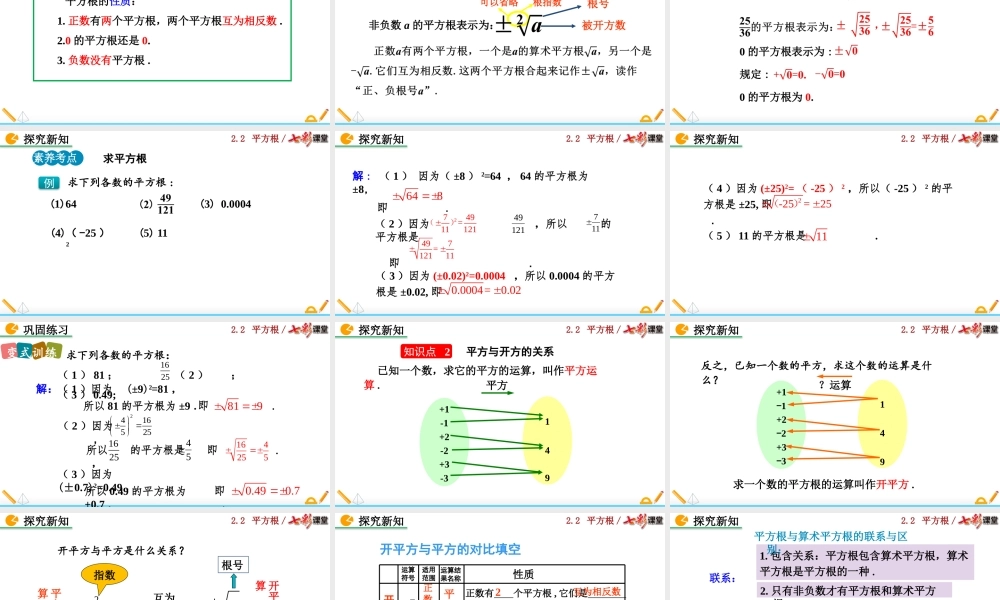
2.2平方根/2.2平方根(第2课时)北师大版数学八年级上册2.2平方根/1.什么叫做算术平方根?导入新知如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.2.2平方根/(1)32=,(-3)2=;(3)0.82=,(-0.8)2=.90.640.643.填空9讨论反过来,如果已知一个数的平方,怎样求这个数?导入新知2.2平方根/1.了解平方根的概念;掌握平方根的特征.2.能正确区分平方根与算术平方根的意义.素养目标3.能利用开平方与平方互为逆运算的关系,求某些非负数的平方根.2.2平方根/问题9的算术平方根是3,也就是说3的平方是9,还有其他数,它的平方等于9吗?3和-3有什么特征?由于(-3)2=9,所以还有,这个数是-3.因此平方等于9的数有两个,3和-3.3和-3互为相反数,会不会是巧合呢?探究新知知识点1平方根的概念和特征2.2平方根/0.87探究新知做一做,想一想2.2平方根/写出左圈和右圈中的“?”表示的数:-11110.60没有x2x8-8??????????-4-0.6641210.360探究新知填一填,想一想2.2平方根/根据上述问题,即要找出一个数,使它的平方等于给定的数.我们抽象出下述概念:例如:(±1)2=1,1的平方根为±1.探究新知一般地,如果有一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根(也叫作二次方根).2.2平方根/1.121的平方根是什么?2.0的平方根是什么?4.-9有没有平方根?为什么?0没有,因为一个数的平方不可能是负数.探究新知±112.2平方根/通过这些题目的解答,你能发现什么?问题(1)正数有几个平方根?(2)0有几个平方根?(3)负数呢?有没有一个数的平方是负数?因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.探究新知2.2平方根/探究新知归纳总结平方根的性质:1.正数有两个平方根,两个平方根互为相反数.2.0的平方根还是0.3.负数没有平方根.2.2平方根/探究新知根号被开方数根指数可以省略知识点2平方根的读法和表示非负数a的平方根表示为:2.2平方根/例如探究新知5的平方根表示为:4的平方根表示为:0的平方根表示为:规定:0的平方根为0.2.2平方根/求下列各数的平方根:(3)0.0004(5)11(4)(2)(1)64探究新知素养考点1求平方根例(-25)22.2平方根/探究新知497=12111(2)因为,所以的平方根是即.121491172749=11121()(3)因为(±0.02)2=0.0004,所以0.0004的平方根是±0.02,即0.0004=0.02解:(1)因为(±8)2=64,64的平方根为±8,即.6482.2平方根/探究新知(4)因为(±25)2=(-25)2,所以(-25)...