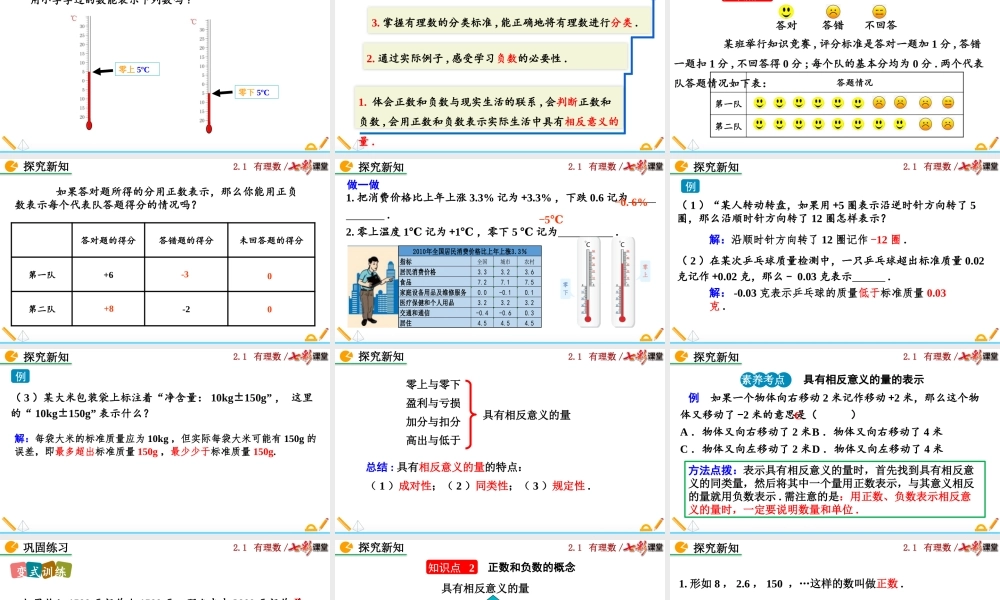
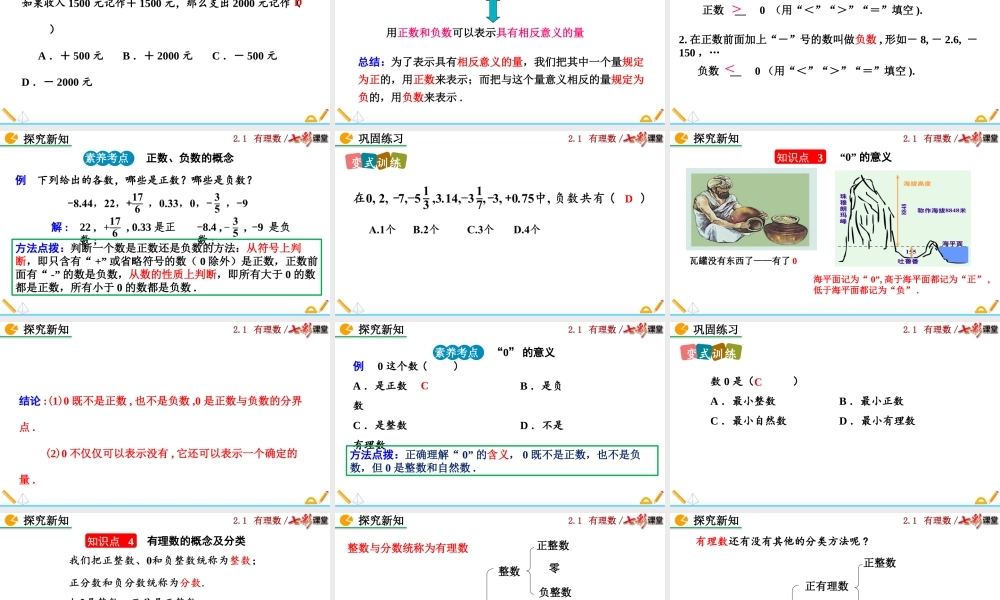
2.1有理数/2.1有理数北师大版数学七年级上册2.1有理数/导入新知零上5ºC零下5ºC用小学学过的数能表示下列数吗?2.1有理数/素养目标2.通过实际例子,感受学习负数的必要性.1.体会正数和负数与现实生活的联系,会判断正数和负数,会用正数和负数表示实际生活中具有相反意义的量.3.掌握有理数的分类标准,能正确地将有理数进行分类.2.1有理数/知识点1用正、负数表示具有相反意义的量探究新知答对答错不回答某班举行知识竞赛,评分标准是答对一题加1分,答错一题扣1分,不回答得0分;每个队的基本分均为0分.两个代表队答题情况如下表:答题情况第一队第二队2.1有理数/如果答对题所得的分用正数表示,那么你能用正负数表示每个代表队答题得分的情况吗?答对题的得分答错题的得分未回答题的得分第一队+6第二队-2-3+800探究新知2.1有理数/探究新知1.把消费价格比上年上涨3.3%记为+3.3%,下跌0.6记为.2.零上温度1℃记为+1℃,零下5℃记为.-0.6%-5℃2010年全国居民消费价格比上年上涨3.3指标居民消费价格食品家庭设备用品及维修服务医疗保健和个人用品交通和通信居住%全国城市农村3.33.23.67.27.17.50.0-0.10.13.23.23.2-0.4-0.60.34.54.54.5做一做2.1有理数/探究新知(1)“某人转动转盘,如果用+5圈表示沿逆时针方向转了5圈,那么沿顺时针方向转了12圈怎样表示?解:沿顺时针方向转了12圈记作-12圈.(2)在某次乒乓球质量检测中,一只乒乓球超出标准质量0.02克记作+0.02克,那么﹣0.03克表示.解:-0.03克表示乒乓球的质量低于标准质量0.03克.例2.1有理数/探究新知(3)某大米包装袋上标注着“净含量:10kg±150g”,这里的“10kg±150g”表示什么?解:每袋大米的标准质量应为10kg,但实际每袋大米可能有150g的误差,即最多超出标准质量150g,最少少于标准质量150g.例2.1有理数/零上与零下盈利与亏损加分与扣分高出与低于具有相反意义的量总结:具有相反意义的量的特点:(1)成对性;(2)同类性;(3)规定性.探究新知2.1有理数/例如果一个物体向右移动2米记作移动+2米,那么这个物体又移动了-2米的意思是()A.物体又向右移动了2米B.物体又向右移动了4米C.物体又向左移动了2米D.物体又向左移动了4米探究新知素养考点具有相反意义的量的表示C方法点拨:表示具有相反意义的量时,首先找到具有相反意义的同类量,然后将其中一个量用正数表示,与其意义相反的量就用负数表示.需注意的是:用正数、负数表示相反意义的量时,一定要说明数量和单位.2.1有理数/巩固...