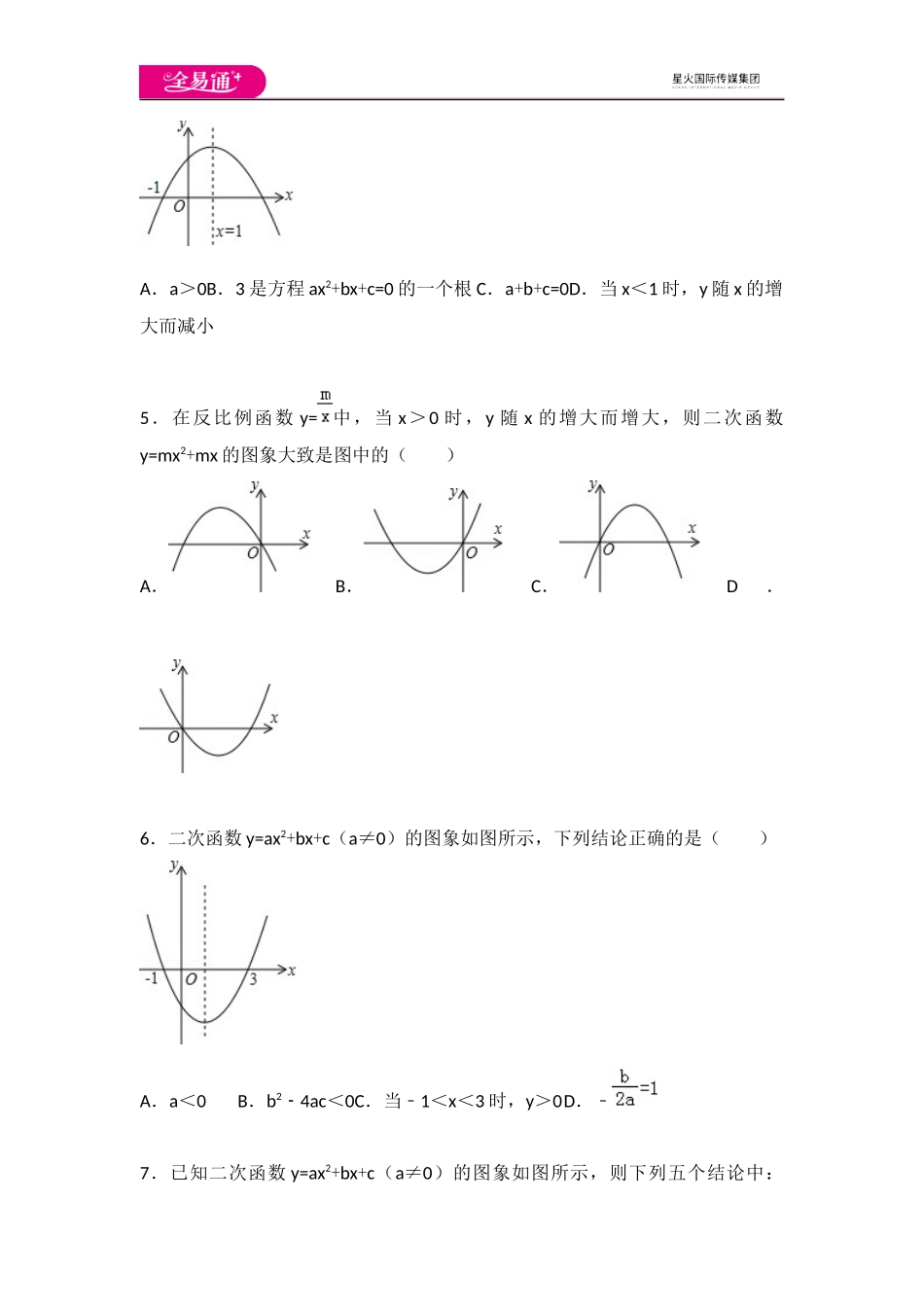
二次函数测试卷(1)一、选择题1.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是()A.a>0B.当﹣1<x<3时,y>0C.c<0D.当x≥1时,y随x的增大而增大2.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是()A.a<0,b<0,c>0,b24ac﹣>0B.a>0,b<0,c>0,b24ac﹣<0C.a<0,b>0,c<0,b24ac﹣>0D.a<0,b>0,c>0,b24ac﹣>03.已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.则其中正确结论的序号是()A.①②B.②③C.①②④D.①②③④4.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是()A.a>0B.3是方程ax2+bx+c=0的一个根C.a+b+c=0D.当x<1时,y随x的增大而减小5.在反比例函数y=中,当x>0时,y随x的增大而增大,则二次函数y=mx2+mx的图象大致是图中的()A.B.C.D.6.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是()A.a<0B.b24ac﹣<0C.当﹣1<x<3时,y>0D.﹣7.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列五个结论中:①a+b+c<0;②ab﹣+c>0;③2ab﹣<0;④abc<0;⑤4a+2b+c>0,错误的个数有()A.1个B.2个C.3个D.4个8.如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(,1),下列结论:①c>0;②b24ac﹣>0;③a+b=0;④4acb﹣2>4a,其中错误的是()A.①B.②C.③D.④9.如图,已知二次函数的图象与x轴的两个交点分别为(﹣1,0),(3,0),对于下列结论:①2a+b=0;②abc<0;③a+b+c>0;④当x>1时,y随x的增大而减小;其中正确的有()A.1个B.2个C.3个D.4个10.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是()A.b24ac﹣>0B.a>0C.c>0D.11.如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=1﹣,且过点(﹣3,0).下列说法:①abc<0;②2ab=0﹣;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是()A.①②B.②③C.①②④D.②③④12.若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列选项正确的是()A.a>0B.c>0C.ac>0D.bc<013.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b24c﹣>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b1﹣)x+c...