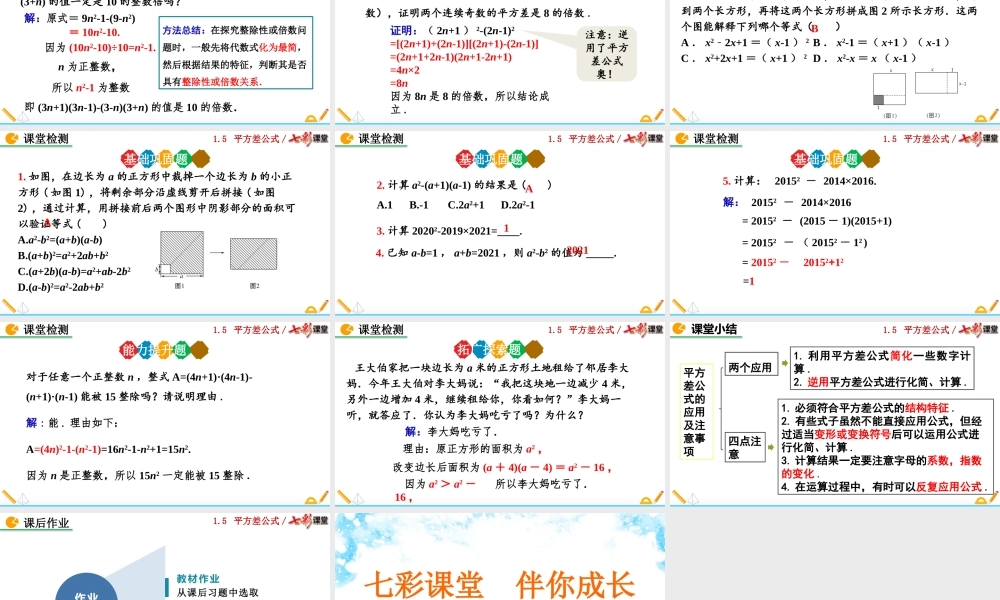
1.5平方差公式/北师大版数学七年级下册1.5平方差公式(第2课时)1.5平方差公式/某同学在计算97×103时将其变成(100-3)(100+3)并很快得出结果,你知道他运用了什么知识吗?这节课我们一起来探讨上述计算的规律.导入新知1.5平方差公式/1.灵活地运用平方差公式进行简便计算.2.了解平方差公式的几何意义,体会数形结合的思想方法.素养目标3.利用平方差公式解答简单问题.1.5平方差公式/如图1,边长为a的大正方形中有一个边长为b的小正方形.ab探究新知知识点平方差公式图11.5平方差公式/(1)请表示图1中的阴影部分的面积.(2)小颖将阴影部分拼成了一个长方形(图2),这个长方形的长和宽分别是多少?你能表示出它的面积吗?a2-b2长=a+b;宽=a-b;面积=(a+b)(a-b)(3)比较(1)(2)的结果,你能验证平方差公式吗?由于(1)(2)表示的面积相同,所以可以验证平方差公探究新知abab图1图21.5平方差公式/(1)计算下列各组算式,并观察它们的共同特点.7×9=8×8=11×13=12×12=79×81=80×80=6364143144639640(2)从以上的过程中,你发现了什么规律?(3)请用字母表示这一规律,你能说明它的正确性吗?(a-1)(a+1)=a2–1平方差公式探究新知1.5平方差公式/解:(1)103×97=(100+3)(100-3)=1002-32=9991(2)118×122=(120-2)(120+2)=1202-22=14396(1)103×97;(2)118×122探究新知用平方差公式进行计算:例1通过合理变形,利用平方差公式,可以简化运算.素养考点1利用平方差公式进行简便运算1.5平方差公式/解:(1)102×98=1002-22=10000–4=(100+2)(100-2)=9996;计算:(1)102×98;(2)51×49;(2)原式=(50+1)(50-1)=502-12=2500–1=2499;巩固练习变式训练1.5平方差公式/探究新知计算:(1)a2(a+b)(a-b)+a2b2(2)(2x-5)(2x+5)-2x(2x-3)例2解:(1)a2(a+b)(a-b)+a2b2=a2(a2-b2)+a2b2=a4-a2b2+a2b2=a4(2)(2x-5)(2x+5)-2x(2x-3)=4x2-52-(4x2-6x)=4x2-25-4x2+6x=6x-25不符合平方差公式运算条件的乘法,按乘法法则进行运算.素养考点2平方差公式在混合运算中的应用1.5平方差公式/计算:(1)(3x+4)(3x-4)-(2x+3)(3x-2)(2)(y+2)(y-2)–(y-1)(y+5).解:(1)原式=(3x)2-42-(6x2+5x-6)(2)原式=y2-22-(y2+4y-5)=y2-4-y2-4y+5=-4y+1.=9x2-16-6x2-5x+6=3x2-5x-10.巩固练习变式训练1.5平方差公式/例3对于任意的正整数n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗?即(3n+1)(3n-1)-(3-n)(3+n)的值是10的倍数.解:原式=9n2-1-(9-n2)=10n2-10.因为(10n2-10)÷10=n2-1.n为正整数,所以n2-1为...