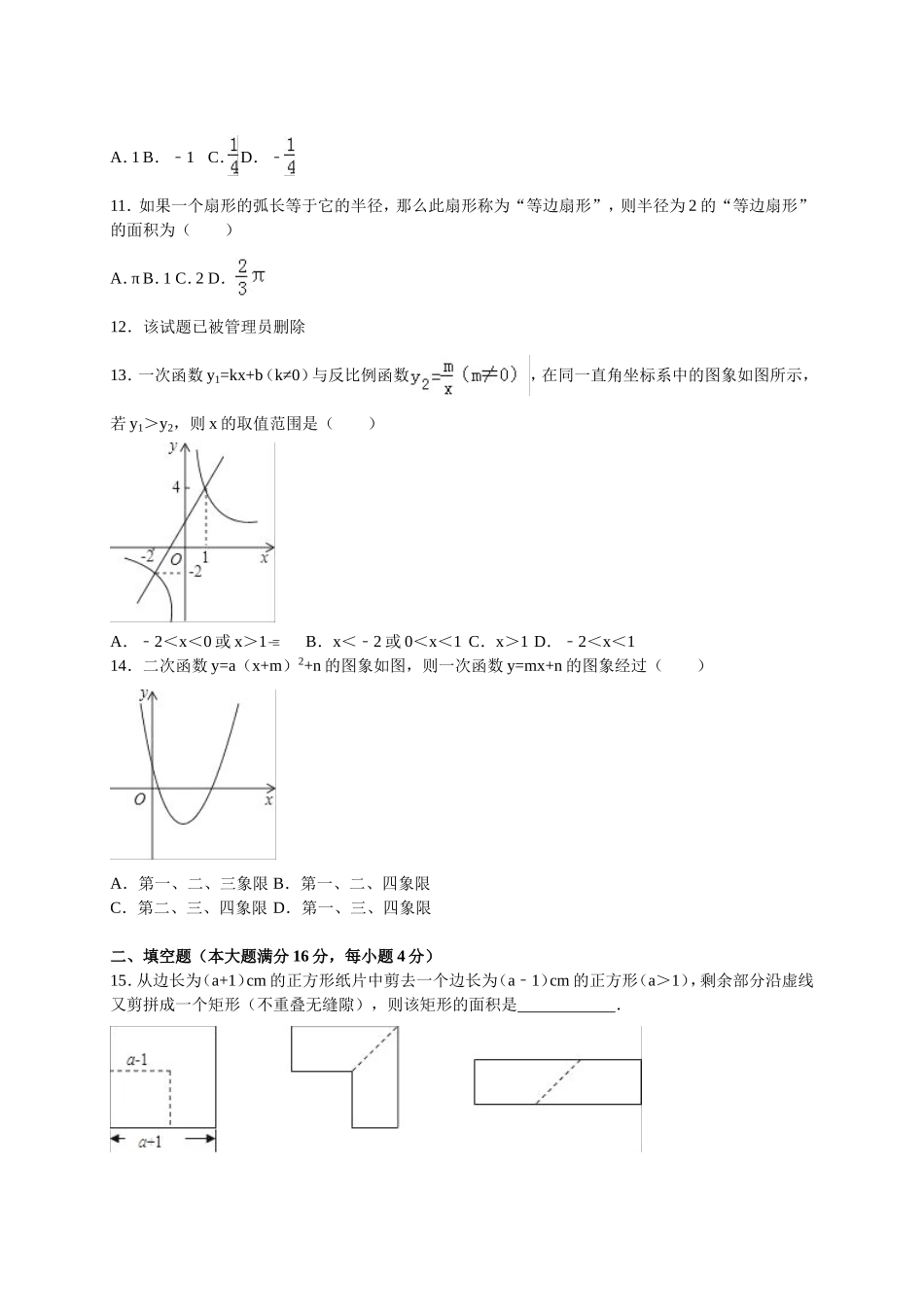
2016届九年级下学期开学考试数学试卷一、选择题(本大题满分42分,每小题3分)1.﹣3的倒数是()A.3B.﹣3C.D.2.已知一粒米的质量是0.000021千克,这个数字用科学记数法表示为()A.21×104﹣千克B.2.1×106﹣千克C.2.1×105﹣千克D.2.1×104﹣千克3.分式方程的解为()A.x=1B.x=2C.x=3D.x=44.今年体育学业考试增加了跳绳测试项目,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).176180184180170176172164186180该组数据的众数、中位数、平均数分别为()A.180,180,178B.180,178,178C.180,178,176.8D.178,180,176.85.如图是一个用相同的小立方体搭成的几何体的三视图,则组成这个几何体的小立方体的个数是()A.2B.3C.4D.56.已知等腰三角形的一个内角为40°,则这个等腰三角形的顶角为()A.40°B.100°C.40°或100°D.70°或50°7.如图,直线lm∥,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为()A.20°B.25°C.30°D.35°8.下列各因式分解正确的是()A.﹣x2+(﹣2)2=(x2﹣)(x+2)B.x2+2x1=﹣(x1﹣)2C.4x24x+1=﹣(2x1﹣)2D.x24x=x﹣(x+2)(x2﹣)9.在平面直角坐标系中,点P(﹣1,2)关于x轴的对称点的坐标为()A.(﹣1,﹣2)B.(1,2)C.(2,﹣1)D.(﹣2,1)10.已知关于x的一元二次方程x2+2xa=0﹣有两个相等的实数根,则a的值是()A.1B.﹣1C.D.﹣11.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为()A.πB.1C.2D.12.该试题已被管理员删除13.一次函数y1=kx+b(k≠0)与反比例函数,在同一直角坐标系中的图象如图所示,若y1>y2,则x的取值范围是()A.﹣2<x<0或x>1B.x<﹣2或0<x<1C.x>1D.﹣2<x<114.二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过()A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限二、填空题(本大题满分16分,每小题4分)15.从边长为(a+1)cm的正方形纸片中剪去一个边长为(a1﹣)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是.16.函数中,自变量x的取值范围是.17.如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为.18.如图,在△ABC中,AB=AC=3cm,AB的垂直平分线交AC于点N,△...