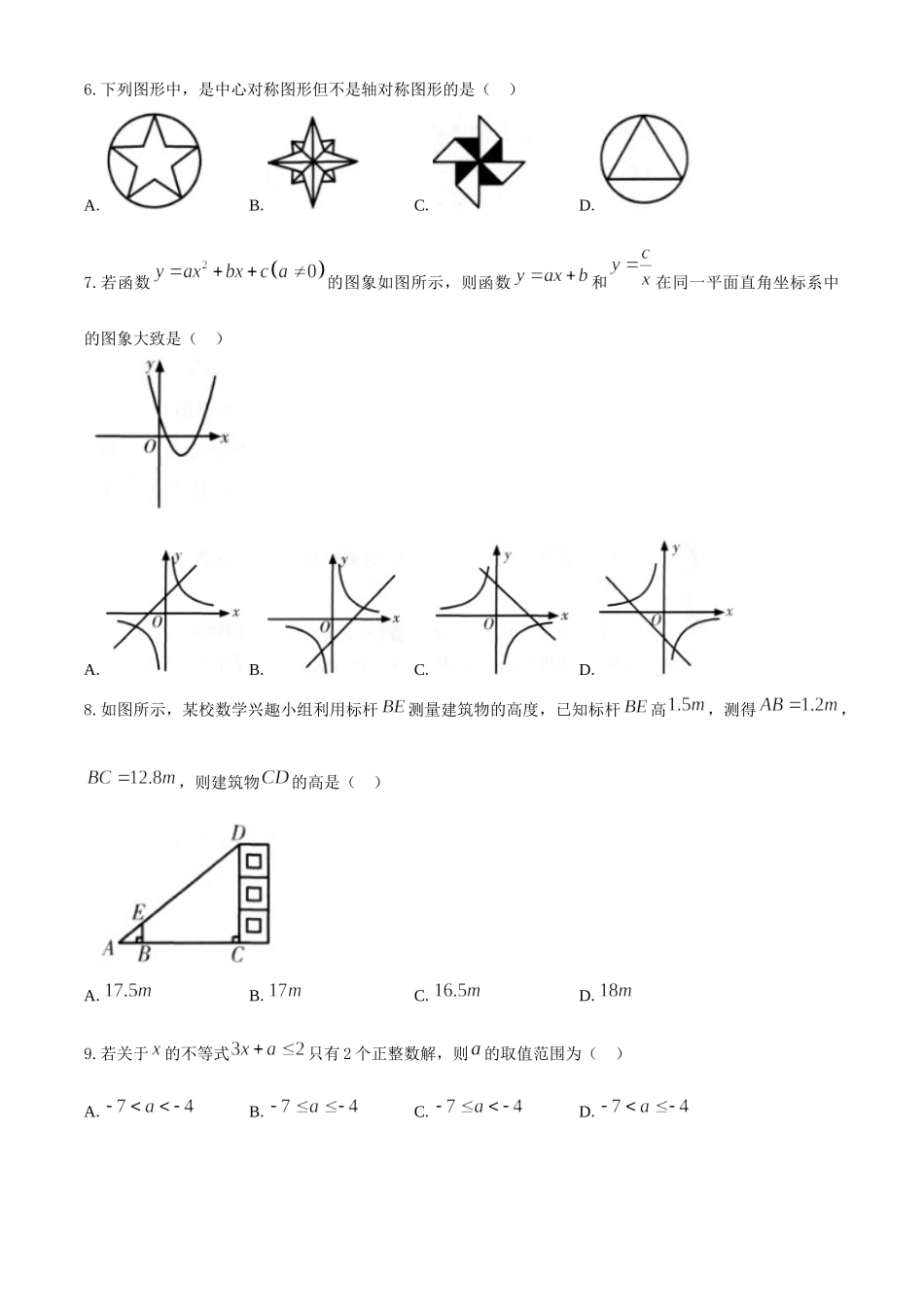
2020年天水市初中毕业与升学学业考试(中考)试卷数学A卷(100分)一、选择题(本大题共10小题,每小题4分,共40分.每小题给出的四个选项中,只有一个选项是正确的,请把正确的选项选出来)1.下列四个实数中,是负数的是()A.B.C.D.2.天水市某网店2020年父亲节这天的营业额为341000元,将数341000用科学记数法表示为()A.B.C.D.3.某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方体中,与“伏”字所在面相对面上的汉字是()A.文B.羲C.弘D.化4.某小组8名学生的中考体育分数如下:39,42,44,40,42,43,40,42.该组数据的众数、中位数分别为()A.40,42B.42,43C.42,42D.42,415.如图所示,、分别与相切于、两点,点为上一点,连接、,若,则的度数为()A.B.C.D.6.下列图形中,是中心对称图形但不是轴对称图形的是()A.B.C.D.7.若函数的图象如图所示,则函数和在同一平面直角坐标系中的图象大致是()A.B.C.D.8.如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高,测得,,则建筑物的高是()A.B.C.D.9.若关于的不等式只有2个正整数解,则的取值范围为()A.B.C.D.10.观察等式:;;;…已知按一定规律排列的一组数:,若,用含的式子表示这组数据的和是()A.B.C.D.二、填空题(本大题共8小题,每小题4分,共32分.只要求填写最后结果)11.分解因式:_________.12.一个三角形的两边长分别为2和5,第三边长是方程的根,则该三角形的周长为_______.13.已知函数,则自变量的取值范围是___________.14.已知,,则的值为_________.15.如图所示,是放置在正方形网格中的一个角,则的值是________.16.如图所示,若用半径为8,圆心角为的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是_________.17.如图所示,将正方形放在平面直角坐标系中,是坐标原点,点的坐标为,则点的坐标为_________.18.如图,在边长为6的正方形内作,交于点,交于点,连接,将绕点顺时针旋转得到.若,则的长为__________.三、解答题(本大题共3小题,共28分.解答时写出必要的文字说明及演算过程)19.(1)计算:.(2)先化简,再求值:,其中.20.为了解天水市民对全市创建全国文明城市工作的满意程度,某中学数学兴趣小组在某个小区内进行了调查统计.将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.请结合图中的信息,解决下列问题:(1)此次调查中接受调查...