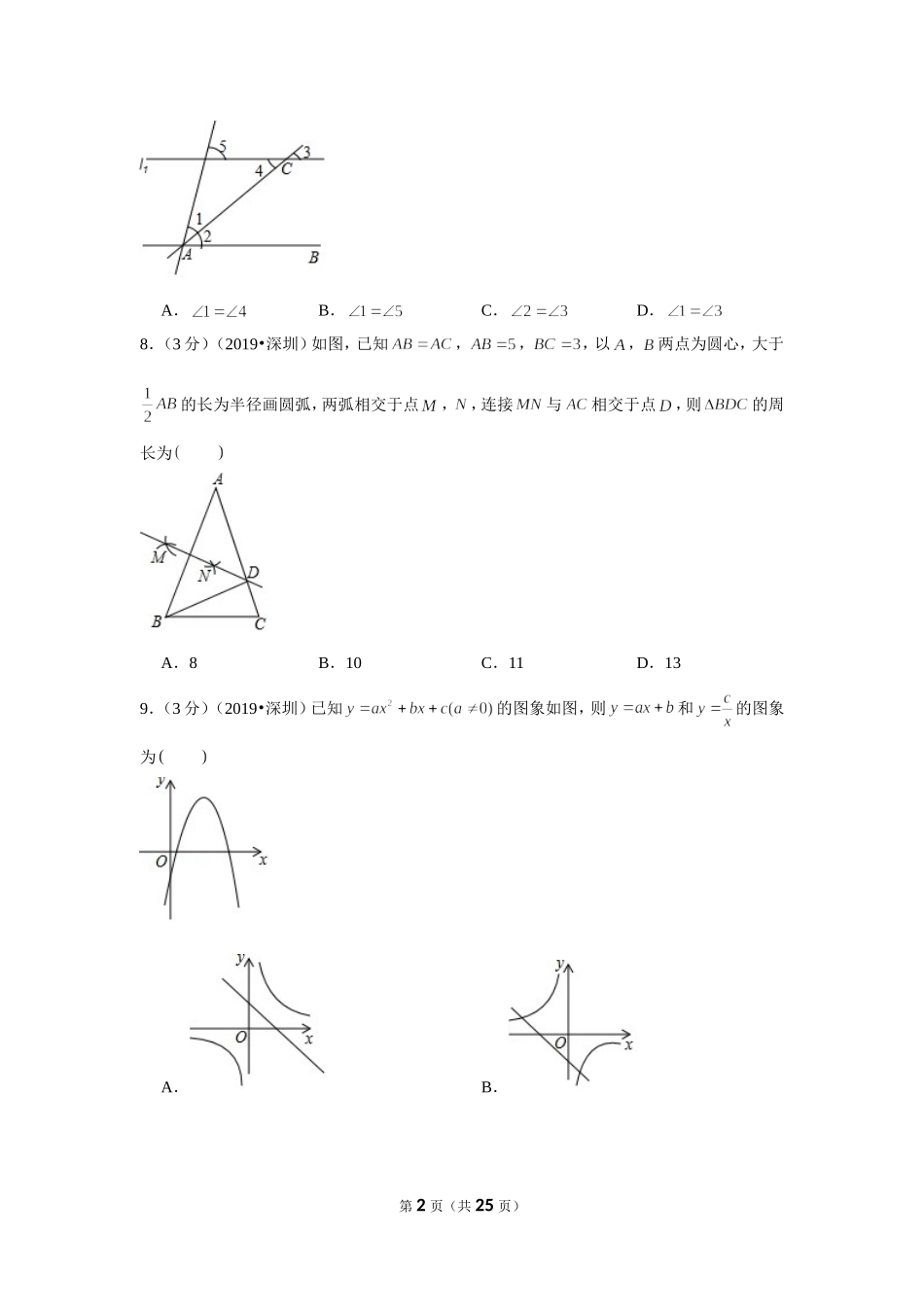
2019年广东省深圳市中考数学试卷一、选择题(每小题3分,共12小题,满分36分)1.(3分)(2019•深圳)的绝对值是A.5B.C.D.2.(3分)(2019•深圳)下列图形中是轴对称图形的是A.B.C.D.3.(3分)(2019•深圳)预计到2025年,中国用户将超过460000000,将460000000用科学记数法表示为A.B.C.D.4.(3分)(2019•深圳)下列哪个图形是正方体的展开图A.B.C.D.5.(3分)(2019•深圳)这组数据20,21,22,23,23的中位数和众数分别是A.20,23B.21,23C.21,22D.22,236.(3分)(2019•深圳)下列运算正确的是A.B.C.D.7.(3分)(2019•深圳)如图,已知,为角平分线,下列说法错误的是第1页(共25页)A.B.C.D.8.(3分)(2019•深圳)如图,已知,,,以,两点为圆心,大于的长为半径画圆弧,两弧相交于点,,连接与相交于点,则的周长为A.8B.10C.11D.139.(3分)(2019•深圳)已知的图象如图,则和的图象为A.B.第2页(共25页)C.D.10.(3分)(2019•深圳)下面命题正确的是A.矩形对角线互相垂直B.方程的解为C.六边形内角和为D.一条斜边和一条直角边分别相等的两个直角三角形全等11.(3分)(2019•深圳)定义一种新运算,例如,若,则A.B.C.2D.12.(3分)(2019•深圳)已知菱形,、是动点,边长为4,,,则下列结论正确的有几个①;②为等边三角形;③;④若,则.A.1B.2C.3D.4二、填空题(每小题3分,共4小题,满分12分)13.(3分)(2019•深圳)分解因式:.14.(3分)(2019•深圳)现有8张同样的卡片,分别标有数字:1,1,2,2,2,3,4,5,将这些卡片放在一个不透明的盒子里,搅匀后从中随机地抽出一张,抽到标有数字2的卡片的概率是.15.(3分)(2019•深圳)如图,在正方形中,,将沿翻折,使点对应点刚好落在对角线上,将沿翻折,使点对应点刚好落在对角线上,求.第3页(共25页)16.(3分)(2019•深圳)如图,在中,,,,点在反比例函数图象上,且轴平分,求.三、解答题(第17题5分,第18题6分,第19题7分,第20题8分,第21题8分,第22题9分,第23题9分,满分52分)17.(5分)(2019•深圳)计算:18.(6分)(2019•深圳)先化简,再将代入求值.19.(7分)(2019•深圳)某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.(1)...