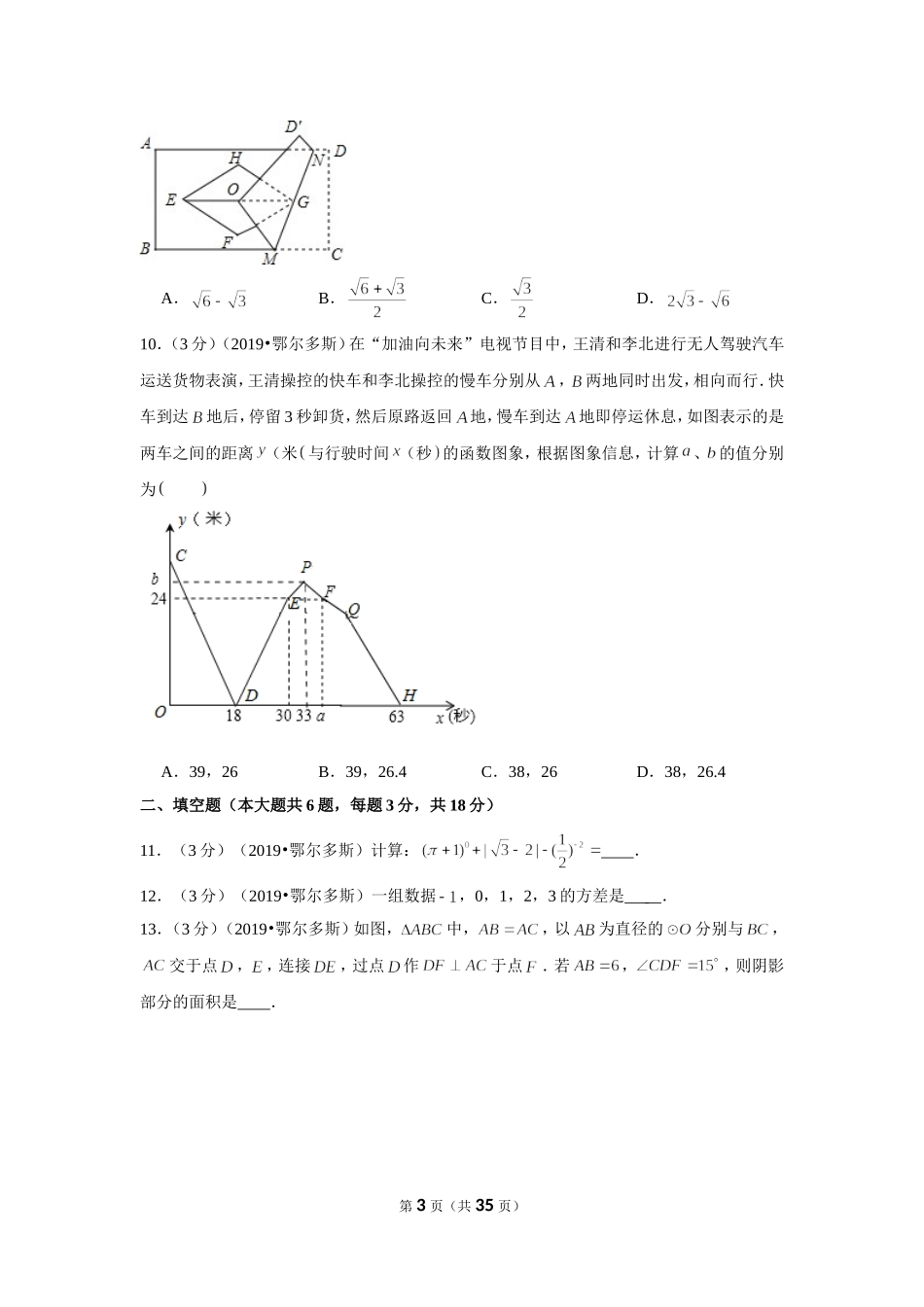
2019年内蒙古鄂尔多斯市中考数学试卷一、单项选择题(本大题共10题,每题3分,共30分)1.(3分)(2019•鄂尔多斯)有理数的相反数为A.B.C.D.32.(3分)(2019•鄂尔多斯)下面四个图形中,经过折叠能围成如图所示的几何图形的是A.B.C.D.3.(3分)(2019•鄂尔多斯)禽流感病毒的半径大约是0.00000045米,它的直径用科学记数法表示为A.米B.米C.米D.米4.(3分)(2019•鄂尔多斯)如图,在正方形的外侧,作等边,则为A.B.C.D.5.(3分)(2019•鄂尔多斯)下列计算①②③④⑤,第1页(共35页)其中任意抽取一个,运算结果正确的概率是A.B.C.D.6.(3分)(2019•鄂尔多斯)下表是抽查的某班10名同学中考体育测试成绩统计表.成绩(分30252015人数(人21若成绩的平均数为23,中位数是,众数是,则的值是A.B.C.2.5D.57.(3分)(2019•鄂尔多斯)如图,在中,,依据尺规作图的痕迹,计算的度数是A.B.C.D.8.(3分)(2019•鄂尔多斯)下列说法正确的是①函数中自变量的取值范围是.②若等腰三角形的两边长分别为3和7,则第三边长是3或7.③一个正六边形的内角和是其外角和的2倍.④同旁内角互补是真命题.⑤关于的一元二次方程有两个不相等的实数根.A.①②③B.①④⑤C.②④D.③⑤9.(3分)(2019•鄂尔多斯)如图,矩形与菱形的对角线均交于点,且,将矩形折叠,使点与点重合,折痕过点.若,,,则的长为第2页(共35页)A.B.C.D.10.(3分)(2019•鄂尔多斯)在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从,两地同时出发,相向而行.快车到达地后,停留3秒卸货,然后原路返回地,慢车到达地即停运休息,如图表示的是两车之间的距离(米与行驶时间(秒的函数图象,根据图象信息,计算、的值分别为A.39,26B.39,26.4C.38,26D.38,26.4二、填空题(本大题共6题,每题3分,共18分)11.(3分)(2019•鄂尔多斯)计算:.12.(3分)(2019•鄂尔多斯)一组数据,0,1,2,3的方差是.13.(3分)(2019•鄂尔多斯)如图,中,,以为直径的分别与,交于点,,连接,过点作于点.若,,则阴影部分的面积是.第3页(共35页)14.(3分)(2019•鄂尔多斯)如果三角形有一边上的中线长等于这边的长,那么称这个三角形为“好玩三角形”.若是“好玩三角形”,且,则.15.(3分)(2019•鄂尔多斯)如图,有一条折线,它是由过,,组成的折...