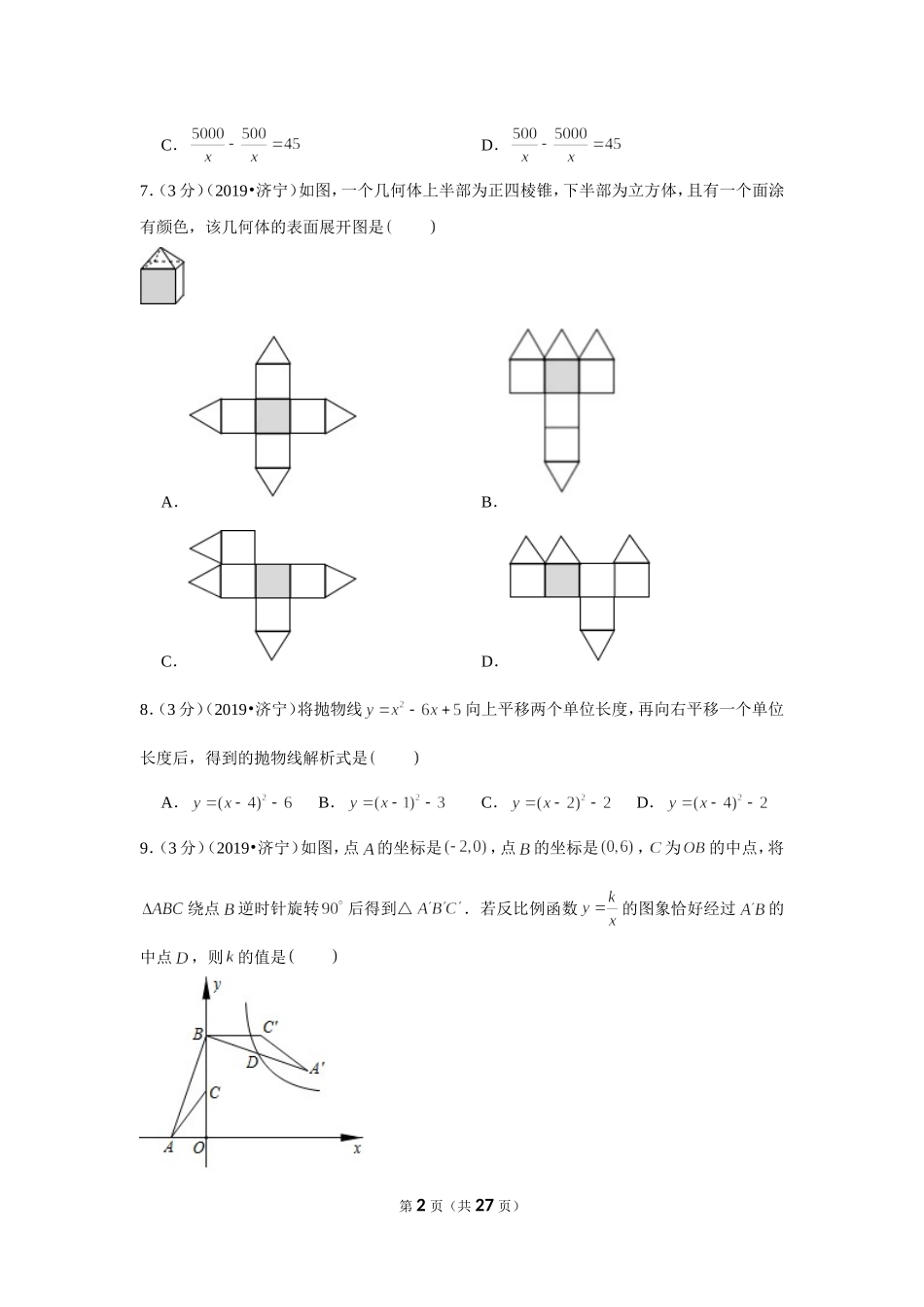
2019年山东省济宁市中考数学试卷一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求1.(3分)(2019•济宁)下列四个实数中,最小的是A.B.C.1D.42.(3分)(2019•济宁)如图,直线,被直线,所截,若,,则的度数是A.B.C.D.3.(3分)(2019•济宁)下列图形中,既是轴对称图形,又是中心对称图形的是A.B.C.D.4.(3分)(2019•济宁)以下调查中,适宜全面调查的是A.调查某批次汽车的抗撞击能力B.调查某班学生的身高情况C.调查春节联欢晚会的收视率D.调查济宁市居民日平均用水量5.(3分)(2019•济宁)下列计算正确的是A.B.C.D.6.(3分)(2019•济宁)世界文化遗产“三孔”景区已经完成基站布设,“孔夫子家”自此有了网络.网络峰值速率为网络峰值速率的10倍,在峰值速率下传输500兆数据,网络比网络快45秒,求这两种网络的峰值速率.设网络的峰值速率为每秒传输兆数据,依题意,可列方程是A.B.第1页(共27页)C.D.7.(3分)(2019•济宁)如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是A.B.C.D.8.(3分)(2019•济宁)将抛物线向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是A.B.C.D.9.(3分)(2019•济宁)如图,点的坐标是,点的坐标是,为的中点,将绕点逆时针旋转后得到△.若反比例函数的图象恰好经过的中点,则的值是第2页(共27页)A.9B.12C.15D.1810.(3分)(2019•济宁)已知有理数,我们把称为的差倒数,如:2的差倒数是,的差倒数是.如果,是的差倒数,是的差倒数,是的差倒数依此类推,那么的值是A.B.7.5C.5.5D.二、填空题:本大题共5小题,每小题3分,共15分。11.(3分)(2019•济宁)已知是方程的一个根,则方程的另一个根是.12.(3分)(2019•济宁)如图,该硬币边缘镌刻的正九边形每个内角的度数是.13.(3分)(2019•济宁)已知点位于第四象限,并且,为整数),写出一个符合上述条件的点的坐标.14.(3分)(2019•济宁)如图,为直角边上一点,以为半径的与斜边相切于点,交于点,已知,.则图中阴影部分的面积是.15.(3分)(2019•济宁)如图,抛物线与直线交于,两点,则不等式的解集是.第3页(共27页)三、解答题:本大题共7小题,共55分,16.(6分)(2019•济宁)计算:17.(7分)(2019•济宁)某校为了解学生课外阅读情...