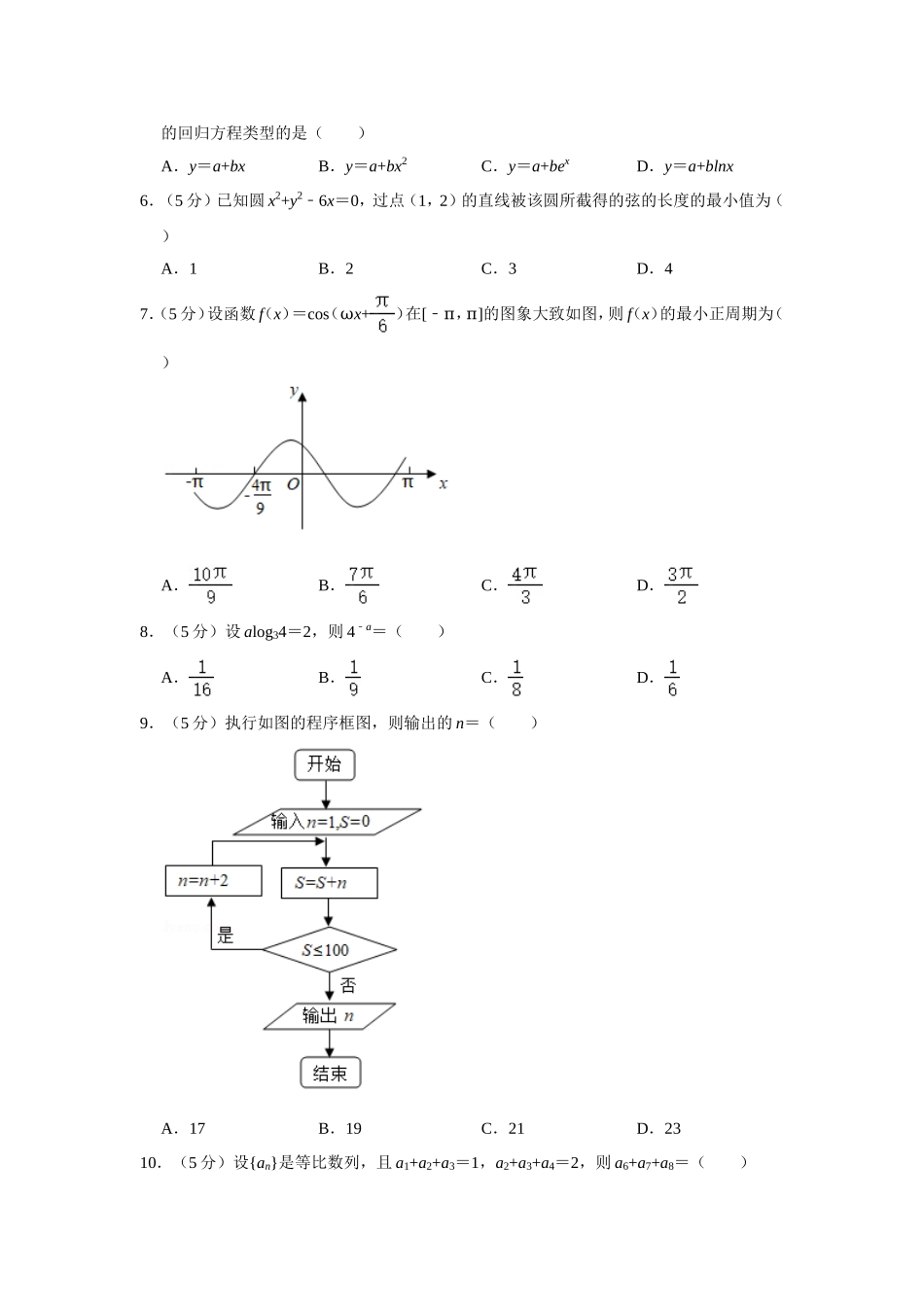
2020年全国统一高考数学试卷(文科)(新课标Ⅰ)一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.(5分)已知集合A={x|x2﹣3x﹣4<0},B={﹣4,1,3,5},则A∩B=()A.{﹣4,1}B.{1,5}C.{3,5}D.{1,3}2.(5分)若z=1+2i+i3,则|z|=()A.0B.1C.D.23.(5分)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为()A.B.C.D.4.(5分)设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为()A.B.C.D.5.(5分)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是()A.y=a+bxB.y=a+bx2C.y=a+bexD.y=a+blnx6.(5分)已知圆x2+y2﹣6x=0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为()A.1B.2C.3D.47.(5分)设函数f(x)=cos(ωx+)在[﹣π,π]的图象大致如图,则f(x)的最小正周期为()A.B.C.D.8.(5分)设alog34=2,则4﹣a=()A.B.C.D.9.(5分)执行如图的程序框图,则输出的n=()A.17B.19C.21D.2310.(5分)设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=()A.12B.24C.30D.3211.(5分)设F1,F2是双曲线C:x2﹣=1的两个焦点,O为坐标原点,点P在C上且|OP|=2,则△PF1F2的面积为()A.B.3C.D.212.(5分)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π二、填空题:本题共4小题,每小题5分,共20分。13.(5分)若x,y满足约束条件则z=x+7y的最大值为.14.(5分)设向量=(1,﹣1),=(m+1,2m﹣4),若⊥,则m=.15.(5分)曲线y=lnx+x+1的一条切线的斜率为2,则该切线的方程为.16.(5分)数列{an}满足an+2+(﹣1)nan=3n﹣1,前16项和为540,则a1=.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22...